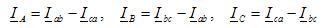Berekening van driefasige circuits

Ketting driefasige wisselstroom bestaat uit een driefasige voeding, een driefasige verbruiker en de communicatiekabels daartussen.

Een symmetrische driefasige voeding kan worden weergegeven als drie enkelfasige voedingen die werken op dezelfde frequentie met dezelfde spanning en met een fasehoek in de tijd van 120 °. Deze bronnen kunnen in ster of driehoek zijn aangesloten.

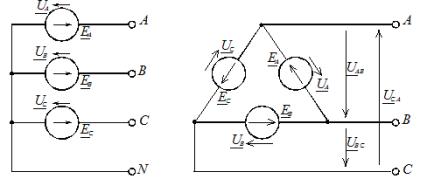
Wanneer verbonden in een ster, wordt het voorwaardelijke begin van de fasen gebruikt om drie lineaire geleiders A, B, C te verbinden, en de uiteinden van de fasen zijn verenigd op één punt, het neutrale punt van de stroombron genoemd (driefasige generator of transformator). Op dit punt kan een nuldraad N worden aangesloten.Het steraansluitschema van de stroombron is weergegeven in figuur 1, a.

Rijst. 1. Aansluitschema's van de voedingsfasen: a — ster; b — driehoek

De spanning tussen lijn en neutrale geleider wordt fase genoemd en tussen lijngeleiders wordt lijn genoemd (voor meer details zie hier - Lijn- en fasespanning).

V geïntegreerde vorm de ingangen van de uitdrukkingen voor de fasespanningen zijn:

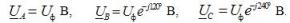
De overeenkomstige lijnspanningen bij sterschakeling:

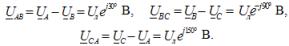
Hier is Uf de fasespanningsmodulus van de stroombron en Ul is de netspanningsmodulus. In een symmetrisch driefasensysteem, wanneer de bronfasen in ster zijn geschakeld, is er een relatie tussen deze spanningen:

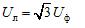
Wanneer de fasen zijn verbonden met een driehoek, zijn de fasevoedingen in serie geschakeld in een gesloten lus (Afbeelding 1, b).

Drie lineaire draden A, B, C worden naar buiten gebracht vanaf de punten waar de bronnen met elkaar worden gecombineerd en gaan naar de belasting. Uit figuur 1, b, is te zien dat de uitgangen van de fasebronnen zijn verbonden met lineaire draden, en daarom, wanneer de fasen van de bron zijn verbonden door een driehoek, zijn de fasespanningen gelijk aan lineair. In dit geval is er geen neutrale draad.

Een belasting kan worden aangesloten op een driefasige voeding. Een driefasige belasting kan qua grootte en aard symmetrisch en asymmetrisch zijn.

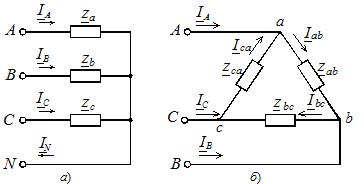
In het geval van een symmetrische belasting zijn de complexe weerstanden van de drie fasen hetzelfde, en als deze weerstanden verschillend zijn, is de belasting onevenwichtig. De belastingsfasen kunnen met elkaar worden verbonden door middel van ster of driehoek (Figuur 2), ongeacht het bronaansluitschema.

Rijst. 2. Aansluitschema's belastingsfasen

De sterverbinding kan met of zonder nuldraad zijn (zie figuur 2, a). De afwezigheid van een neutrale draad elimineert de starre verbinding van de belastingsspanning met de voedingsspanning, en in het geval van een asymmetrische fasebelasting zijn deze spanningen niet gelijk aan elkaar.Om ze te onderscheiden, hebben we afgesproken om hoofdletters te gebruiken in de letteraanduidingsindexen van de voedingsspanningen en -stromen, en kleine letters in de belastingspecifieke parameters.

Het algoritme voor het analyseren van een driefasig circuit hangt af van het belastingsaansluitschema, de initiële parameters en het doel van de berekening.

De methode met twee knooppunten wordt gebruikt om de fasespanningen te bepalen met een ongebalanceerde stergekoppelde belasting zonder nulleider. Volgens deze methode begint de berekening met het bepalen van de spanning UN tussen de neutrale punten van de voeding en de belasting, de neutrale afwijkingsspanning genoemd:

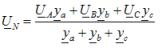
waar ya, yb, yc — toegestane waarden van de overeenkomstige belastingsfasen in complexe vorm

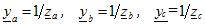
De spanningen over de fasen van een ongebalanceerde belasting worden gevonden uit de uitdrukkingen:

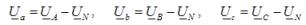
In het speciale geval van belastingonbalans, wanneer er bij afwezigheid van een neutrale geleider een kortsluiting optreedt in een van de belastingsfasen, is de neutrale voorspanning gelijk aan de fasespanning van de voeding van de fase waarin de kortsluiting heeft plaatsgevonden.

De spanning op de gesloten fase van de belasting is nul en op de andere twee is deze numeriek gelijk aan de lijnspanning. Stel bijvoorbeeld dat er een kortsluiting optreedt in fase B. De neutrale voorspanning is in dit geval UN = UB. Dan de fasespanningen op de belasting:

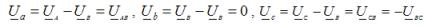
Fasestromen in de belasting, het zijn ook lijngeleiderstromen voor elk type belasting:

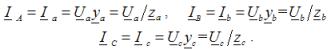
Bij de taken bij het berekenen van driefasige circuits worden drie opties overwogen voor het verbinden van driefasige consumenten met een ster: aansluiting op een neutrale draad in aanwezigheid van consumenten in drie fasen, aansluiting op een neutrale draad bij afwezigheid van consumenten in één van de fasen, en aansluiting zonder nuldraad met een korte verbinding in een van de belastingsfasen...

In de eerste en tweede versie bevinden de overeenkomstige fasespanningen van de voeding zich op de belastingsfasen en worden de fasestromen in de belasting bepaald door de bovenstaande formules.

In de derde versie is de spanning van de belastingsfasen niet gelijk aan de fasespanning van de voeding en wordt bepaald met behulp van de afhankelijkheden

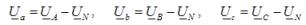
De stromen in twee niet-kortgesloten fasen worden bepaald volgens de wet van Ohm, als een fractie van de deling van de fasespanning door de impedantie van de respectieve fase. De kortsluitstroom wordt bepaald met behulp van een vergelijking op basis van De eerste wet van Kirchhoffopgesteld voor het neutrale punt van de last.

Voor het bovenstaande voorbeeld van een kortsluiting in fase B:

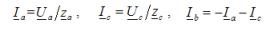
Voor elk type belasting zijn de driefasige actieve en reactieve vermogens gelijk aan de som van de respectievelijke actieve en blinde vermogens van de afzonderlijke fasen. Om deze fasevermogens te bepalen, kunt u de uitdrukking gebruiken

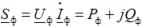
waarbij Uf,Azf, het complex is van de spanning en het complex van gekoppelde stromen in de belastingsfase; Pf, Qf — actief en reactief vermogen in de belastingsfase.

Driefasig actief vermogen: P = Pa + Pb + Pc

Blindvermogen in drie fasen: Q = Qa + Qb + Vc

Driefasig schijnbaar vermogen:

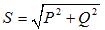
Wanneer consumenten zijn verbonden door een driehoek, heeft het circuit de vorm zoals weergegeven in figuur 2, b. In deze modus is de fase-aansluiting van de gebalanceerde voeding niet relevant.

Spanningen tussen de voedingslijnen worden gedetecteerd op de belastingsfasen. De fasestromen in de belasting worden bepaald met behulp van De wet van Ohm voor een deel van een circuitAzf = Uf /zf, waarbij Uf — fasespanning in de belasting (overeenkomend met de netspanning van de stroombron); zf is de totale weerstand van de overeenkomstige fase van de belasting.

Stromen in lineaire geleiders worden bepaald door fasestromen op basis van de eerste wet van Kirchhoff voor elk knooppunt (punten a, b, c) van het circuit weergegeven in figuur 2, b: