Berekening van spanningsvalnetwerken

Verbruikers van elektrische energie werken normaal wanneer hun terminals worden voorzien van de spanning waarvoor de gegeven elektrische motor of apparaat is ontworpen. Wanneer elektriciteit via draden wordt verzonden, gaat een deel van de spanning verloren door de weerstand van de draden, en als gevolg daarvan is aan het einde van de lijn, dat wil zeggen bij de consument, de spanning lager dan aan het begin van de lijn .

Een verlaging van de verbruikersspanning in vergelijking met normaal heeft invloed op de werking van de stroomafnemer, of het nu gaat om stroom- of verlichtingsbelastingen. Daarom mogen spanningsafwijkingen bij het berekenen van een hoogspanningslijn de toegestane normen niet overschrijden, netwerken die zijn geselecteerd uit de huidige belasting en bedoeld zijn voor verwarming, worden in de regel gecontroleerd door spanningsverlies.

Spanningsverlies ΔU heet het verschil in spanning aan het begin en einde van de lijn (sectie van de lijn). Het is gebruikelijk om ΔU in relatieve eenheden te specificeren - relatief ten opzichte van de nominale spanning. Analytisch wordt het spanningsverlies bepaald door de formule:

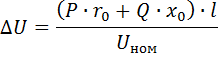
waar P — actief vermogen, kW, Q — reactief vermogen, kvar, weerstand van ro — lijn, Ohm / km, xo — inductieve weerstand van lijn, Ohm / km, l — lengte van lijn, km, Unom — nominale spanning , kv.

De waarden van actieve en inductieve weerstand (Ohm / km) voor bovenleidingen gemaakt met draad A-16 A-120 worden gegeven in de referentietabellen. De actieve weerstand van 1 km aluminium (klasse A) en staal-aluminium (klasse AC) geleiders kan ook worden bepaald met de formule:

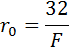
waarbij F de doorsnede is van de aluminiumdraad of de doorsnede van het aluminium deel van de AC-draad, mm2 (er wordt geen rekening gehouden met de geleidbaarheid van het stalen deel van de AC-draad).

Volgens PUE ("Regels voor elektrische installaties") mag de spanningsafwijking van normaal voor elektriciteitsnetwerken niet meer dan ± 5% bedragen, voor elektrische verlichtingsnetwerken van industriële ondernemingen en openbare gebouwen - van +5 tot - 2,5%, voor woningen elektrische verlichtingsnetwerken gebouwen en buitenverlichting ± 5%. Bij het berekenen van de netwerken gaan ze uit van het toegestane spanningsverlies.

Rekening houdend met de ervaring met het ontwerp en de werking van elektrische netwerken, worden de volgende toegestane spanningsverliezen genomen: voor laagspanning - van de bussen van de transformatorruimte tot de verste verbruiker - 6%, en dit verlies wordt ongeveer als volgt verdeeld : van het station of step-down transformatorstation tot de ingang van het pand, afhankelijk van de belastingsdichtheid - van 3,5 tot 5%, van de ingang tot de verst verwijderde gebruiker - van 1 tot 2,5%, voor hoogspanningsnetwerken tijdens normale werking op kabelnetwerken - 6%, in overhead - 8%, in noodmodus van het netwerk in kabelnetwerken - 10% en in antenne - 12%.

Er wordt aangenomen dat driefasige driedraadslijnen met een spanning van 6-10 kV werken met een uniforme belasting, dat wil zeggen dat elk van de fasen van een dergelijke lijn gelijkmatig wordt belast. In laagspanningsnetwerken kan het vanwege de verlichtingsbelasting moeilijk zijn om een ​​gelijkmatige verdeling tussen de fasen te bereiken, daarom wordt daar meestal een 4-draads systeem met draaistroom 380/220 V gebruikt. systeem, elektromotoren zijn aangesloten op lineaire draden en verlichting wordt verdeeld tussen lijn- en neutrale draden. Op deze manier wordt de belasting van de drie fasen vereffend.

Bij de berekening kunt u zowel de aangegeven vermogens gebruiken als de waarden van de stromen die overeenkomen met deze vermogens.In lijnen met een lengte van enkele kilometers, wat met name geldt voor lijnen met een spanning van 6-10 kV, is het noodzakelijk om rekening te houden met de invloed van de inductieve weerstand van de draad op het spanningsverlies in de lijn.

Voor berekeningen kan worden aangenomen dat de inductieve weerstand van koper- en aluminiumdraden gelijk is aan 0,32-0,44 Ohm / km, en de lagere waarde moet worden genomen op kleine afstanden tussen de draden (500-600 mm) en doorsneden van de draad over 95 mm2, en meer bij afstanden van 1000 mm en meer en doorsneden 10-25 mm2.

Het spanningsverlies in elke geleider van een driefasige lijn, rekening houdend met de inductieve weerstand van de geleiders, wordt berekend met de formule

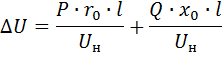
waarbij de eerste term aan de rechterkant de actieve component is en de tweede de reactieve component van het spanningsverlies.

De procedure voor het berekenen van het spanningsverlies van een hoogspanningslijn met geleiders van non-ferrometalen, rekening houdend met de inductieve weerstand van de geleiders, is als volgt:

1. We stellen de gemiddelde waarde van inductieve weerstand voor aluminium of staal-aluminiumdraad in op 0,35 Ohm / km.

2. We berekenen de actieve en reactieve belastingen P, Q.

3. Bereken het reactieve (inductieve) spanningsverlies

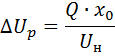
4. Het toegestane actieve spanningsverlies wordt gedefinieerd als het verschil tussen het gespecificeerde netwerkspanningsverlies en het reactieve spanningsverlies:

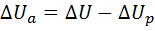
5. Bepaal de doorsnede van de draad s, mm2

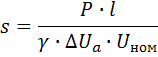
waarbij γ het omgekeerde is van de specifieke weerstand ( γ = 1 / ro - specifieke geleidbaarheid).

6. We kiezen de dichtstbijzijnde standaardwaarde van s en vinden daarvoor de actieve en inductieve weerstand op 1 km van de lijn (ro, NS).

7. Bereken de bijgewerkte waarde spanningsverlies volgens de formule.

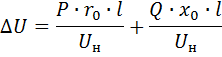
De resulterende waarde mag het toegestane spanningsverlies niet overschrijden.Als het acceptabeler bleek te zijn, moet je een draad nemen met een grotere (volgende) sectie en deze opnieuw berekenen.

Voor DC-lijnen is er geen inductieve weerstand en zijn de bovenstaande algemene formules vereenvoudigd.

Berekening van netwerken NS constant stroomspanningsverlies.

Laat het vermogen P, W worden overgedragen langs een lijn van lengte l, mm, dit vermogen komt overeen met de stroom

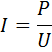
waarbij U de nominale spanning is, V.

Draadweerstand aan beide uiteinden

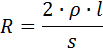
waar p de specifieke weerstand van de geleider is, is s de dwarsdoorsnede van de geleider, mm2.

Verlies van netspanning

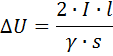
De laatste uitdrukking maakt het mogelijk om een ​​computationele berekening te maken van het spanningsverlies in een bestaande lijn wanneer de belasting bekend is, of om de doorsnede van de geleider voor een gegeven belasting te kiezen

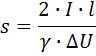
Berekening van enkelfasige AC-netwerken voor spanningsverliezen.

Als de belasting puur actief is (verlichting, verwarmingstoestellen, enz.), wijkt de berekening niet af van de bovenstaande constante lijnberekening. Als de belasting gemengd is, d.w.z. de arbeidsfactor verschilt van één, dan hebben de berekeningsformules de vorm:

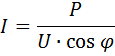
netspanningsverlies

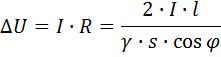
en het vereiste deel van de lijngeleider

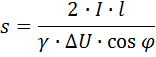
Voor een distributienetwerk met een spanning van 0,4 kV, dat proceslijnen en andere elektrische ontvangers van hout- of houtbewerkingsbedrijven voedt, wordt het ontwerpschema opgesteld en wordt het spanningsverlies berekend voor individuele secties. Gebruik voor het gemak van berekeningen in dergelijke gevallen speciale tabellen. Laten we een voorbeeld geven van zo'n tabel, die de spanningsverliezen weergeeft in een driefasige bovenleiding met aluminium geleiders met een spanning van 0,4 kV.

Spanningsverliezen worden bepaald door de volgende formule:

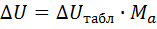
waarbij ΔU—spanningsverlies, V, ΔUsectie — waarde van relatieve verliezen,% per 1 kW • km, Ma — het product van het uitgezonden vermogen P (kW) door de lengte van de lijn, kW • km.