Berekening van potentiometer en samengestelde shunt

Concepten en formules

Een potentiometer is een variabele weerstand met een schuif die wordt meegeleverd zoals weergegeven in afb.

Voor meer details zie — Potentiometers en hun toepassingen

Op de punten 1 en 2 wordt een spanning U aangelegd. Van de punten 2 en 3 wordt een instelbare spanning verwijderd, waarvan de waarde kleiner is dan U en afhankelijk is van de stand van de schuifregelaar. Spanningsdelers hebben een soortgelijk schema, maar ze zijn niet verstelbaar en hebben geen beweegbare schuifregelaar.

Potentiometers, spanningsdelers en complexe shunts worden berekend met behulp van wetten van Kirchhoff, zoals de berekening van conventionele circuits met weerstanden.

Voorbeelden van

1. De bronspanning is U = 24 V, de totale weerstand van de potentiometer is r = 300 Ohm. De motor wordt apart gemonteerd zodat r1 = 50 Ohm. Welke spanning U1 kan worden verwijderd uit de punten 3 en 2 (fig. 1)?

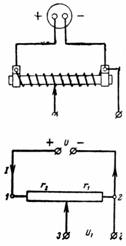
Rijst. 1.

De stroom I en de spanning U over de weerstand r zijn gerelateerd aan de formule I ∙ r = U.

De schuifregelaar van de potentiometer scheidt een deel van de weerstand, dwz. de weerstand r1. De spanningsval tussen de punten 3 en 2 is gelijk aan I ∙ r1 = U1.

Uit de verhouding van de spanningsval verkrijgen we de gelijkheid (I ∙ r1) / (I ∙ r) = U1 / U. Hoe groter de weerstand r1, hoe groter de waarde van de spanning U1 tussen punten 3 en 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. De potentiometer (fig. 2) wordt belast op een lamp met een weerstand r = 100 Ohm. De potentiometer wordt door een schuif in twee delen gedeeld met r1 = 600 Ohm en r2 = 200 Ohm. Bepaal de spanning Ul en de lampstroom Il.

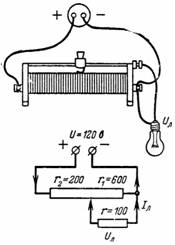
Rijst. 2.

Stroom I vloeit door weerstand r2 en stroom Il vloeit door de lamp. Door de weerstand r1 vloeit een stroom I-Il, waardoor over de weerstand r1 een spanning ontstaat die gelijk is aan de lampspanning: (I-Il) ∙ r1 = Ul.

Aan de andere kant is de lampspanning gelijk aan de bronspanning minus spanningsval bij weerstand r2: U-I ∙ r2 = Ul.

De stroom I is gelijk aan de bronspanning gedeeld door de resulterende weerstand van de serie-parallelschakeling van de weerstanden:

ik = U / (r2 + (r ∙ r1) / (r + r1)).

We vervangen de uitdrukking voor de totale stroom van de bron in de tweede vergelijking:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Na de transformatie krijgen we een uitdrukking voor de lampspanning:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Als we deze uitdrukking transformeren, uitgaande van het feit dat Ul = Il ∙ r, dan krijgen we een uitdrukking voor de lampstroom:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Vervang de numerieke waarden in de resulterende vergelijkingen:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul / r = 36/100 = 0,36 A.

3. Bereken de spanning Up en de stroom Ip van het meetapparaat dat op een deel van de potentiometer is aangesloten. Het apparaat heeft een weerstand van r = 1000 Ohm. Het vertakkingspunt verdeelt de weerstand van de verdeler in r2 = 500 ohm en r1 = 7000 ohm (fig. 3).Spanning op de klemmen van de potentiometer U = 220 V.

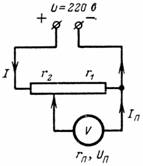
Rijst. 3.

Met behulp van de eerder verkregen formules kunnen we schrijven dat de stroom die door het apparaat vloeit, is:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 1000)= 1540000/11000000 = 1,54 / 11 = 0,14 A.

Omhoog = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Bereken de spanning van het apparaat Up, als het een stroom verbruikt Ip = 20 mA en is aangesloten op een potentiometer verdeeld in weerstanden r2 = 10 ^ 4 Ohm en r1 = 2 ∙ 10 ^ 4 Ohm (Fig. 3).

De totale spanning in de spanningsdeler is gelijk aan de som van de spanningsdalingen in zijn delen (door weerstanden r1 en r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Omhoog

De bronstroom is vertakt op het contactpunt van de motor: I = I1 + Ip; ik = Upn / r1 + In.

We vervangen de waarde van de stroom I in de spanningsvergelijking:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Daarom is de apparaatspanning Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Vervang de numerieke waarden: Up = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.

5. Een gelijkstroombron met spanning U = 120 V voedt de anodecircuits van de radio-ontvanger via een potentiometer (spanningsdeler), die samen met het filter een weerstand heeft van r = 10000 Ohm. De spanning U1 wordt verwijderd door de weerstand r2 = 8000 Ohm. Bereken de anodespanning bij nullast en bij belastingsstroom I = 0,02 A (fig. 4).

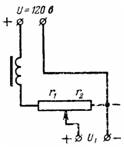
Rijst. 4.

Het eerste geval is vergelijkbaar met voorbeeld 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

Het tweede geval is vergelijkbaar met voorbeeld 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Tijdens het opladen zakt de spanning van 96 naar 64 V.Als er meer spanning nodig is, moet de schuifregelaar naar links worden verplaatst, dat wil zeggen dat de weerstand r2 moet worden verhoogd.

6. Spanningen Ua en Ub worden verwijderd door de spanningsdeler. De totale weerstand van de spanningsdeler aangesloten op de spanning U1 = 220 V is r = 20.000 Ohm. Wat is de spanning Ua in de weerstand r3 = 12000 Ohm bij stroomverbruik Ia = 0,01 A en de spanning Ub in de weerstand r2 + r3 = 18000 Ohm bij stroomverbruik Ib = 0,02 A (fig. 5).

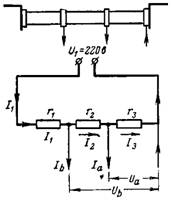
Rijst. 5.

Spanningsweerstand r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

De spanning Ub is gelijk aan de som van de spanningsval Ua over de weerstand r3 en de spanningsval over de weerstand r2. De spanningsval over weerstand r2 is gelijk aan I2 ∙ r2. Stroom I2 = Ia + I3. De stroom I3 kan worden berekend zoals in voorbeeld 1:

I3 = (220-80-40) / 20.000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Spanning Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

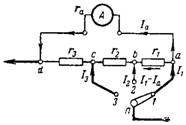
7. Bereken de gecombineerde shunt voor de milliampèremeter zodat deze bij verschillende standen van de schakelaar de volgende meetbereiken heeft: I1 = 10 mA; I2 = 30mA; I3 = 100mA. Het shuntaansluitschema wordt getoond in Fig. 6. Interne weerstand van het apparaat ra = 40 Ohm. Intrinsiek meetbereik van milliampèremeter 2 mA.

Rijst. 6.

Bij het meten van stroom I≤2mA is de shunt uitgeschakeld.

a) Bij het meten van de stroom I = 10 mA staat de schakelaar in stand 1 en vloeit er een stroom van 10-2 = 8 mA door alle shuntweerstanden. De spanningsval over de shuntweerstand Ush en het apparaat Ua tussen de punten d en a moet gelijk zijn

Ush = Ua;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Bij het meten van stroom I2 = 30 mA staat de schakelaar in stand 2. De gemeten stroom deelt zich bij punt b. Bij volledige afbuiging van de wijzer van het apparaat zal de stroom Ia = 2 mA door de weerstand r1 en het apparaat ra gaan.

De rest van de stroom I2-Ia gaat door de weerstanden r2 en r3. De stromen zullen dezelfde spanningsval veroorzaken over de twee takken tussen de punten d en b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) Op een vergelijkbare manier zullen we de berekening uitvoeren bij het vergroten van het meetbereik tot I3 = 100 mA. Stroom I3-Ia zal door weerstand r3 vloeien en stroom Ia door weerstanden r1, r2, ra. De spanning in beide takken is gelijk: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

We hebben drie vergelijkingen verkregen met drie onbekende weerstandswaarden r1, r2 en r3.

We vermenigvuldigen alle vergelijkingen met 1000 en rekenen ze om:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

Laten we de eerste en derde vergelijkingen toevoegen: 50 ∙ r3 = 50;

r3 = 50/50 = 1 Ohm.

Laten we de eerste en tweede vergelijkingen optellen: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 ohm.

Laten we de verkregen resultaten in de eerste vergelijking vervangen: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 ohm.

De juistheid van de berekening kan worden gecontroleerd door de verkregen weerstandswaarden in de vergelijkingen te vervangen.