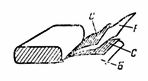
Berekening van condensatorcapaciteit

Capaciteit C is het vermogen van de condensator om de hoeveelheid elektriciteit Q in ampère-seconden of de lading Q in hangers te accepteren (op te slaan en vast te houden). Als je een lichaam, bijvoorbeeld een bal, een elektrische lading (hoeveelheid elektriciteit) Q vertelt, dan zal een elektroscoop die tussen dit lichaam en de aarde is aangesloten een spanning U aangeven (fig. 1). Deze spanning is evenredig met de lading en hangt ook af van de vorm en grootte van het lichaam.

De relatie tussen lading Q en spanning U wordt uitgedrukt door de formule Q = C ∙ U.

De evenredigheidsconstante C wordt de capaciteit van het lichaam genoemd. Als het lichaam de vorm van een bal heeft, is de capaciteit van het lichaam evenredig met de straal van de bal r.

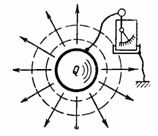
Rijst. 1.

De maateenheid voor capaciteit is de farad (F).

Het lichaam heeft een capaciteit van 1 F wanneer een lading van 1 k een spanning van 1 V opwekt tussen het lichaam en de aarde. Farads zijn een zeer grote meeteenheid, dus in de praktijk worden kleinere eenheden gebruikt: microfarad (μF), nanofarad (nF) en picofarad (pF)...

Deze eenheden zijn gerelateerd aan de volgende verhoudingen: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

De capaciteit van een bal met een straal van 1 cm is 1,1 pF.

Niet alleen een geïsoleerd lichaam kan lading verzamelen, maar ook een speciaal apparaat dat een condensator wordt genoemd. Een condensator bestaat uit twee of meer platen (platen) die gescheiden zijn door een diëlektricum (isolatie).

In afb. 2 toont een schakeling met een gelijkstroombron aangesloten op een condensator. Bij het inschakelen wordt een positieve lading +Q gevormd in de rechterplaat van de condensator en een negatieve lading –Q in de linkerplaat. Tijdens condensator lading er stroomt een stroom door het circuit, dat stopt na het einde van het opladen; dan is de spanning over de condensator gelijk aan e. enz. C. bron U. De lading op de condensatorplaat, spanning en capaciteit zijn gerelateerd door de verhouding Q = C ∙ U. In dit geval wordt een elektrostatisch veld gevormd in het diëlektricum van de condensator.

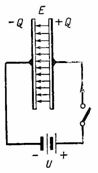
Rijst. 2.

De capaciteit van een condensator met een luchtdiëlektricum kan worden berekend met de formule C = S / (4 ∙ π ∙ d) ∙ 1.11, pF, waarbij S de oppervlakte is van één plaat, cm2; d is de afstand tussen de platen, cm; C is de capaciteit van de condensator, pF.

De capaciteit van een condensator bestaande uit n platen (fig. 3) is gelijk aan: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

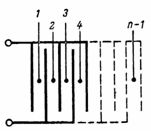
Rijst. 3.

Als de ruimte tussen de platen gevuld wordt met een ander diëlektricum, bijvoorbeeld papier, zal de capaciteit van de condensator toenemen met een factor ε. Wanneer papierisolatie wordt gebruikt, neemt de capaciteit 3 ​​keer toe, met mica-isolatie - 5-8 keer, met glas - 7 keer, enz. De waarde van ε wordt de diëlektrische constante van het diëlektricum genoemd.

De algemene formule voor het bepalen van de capaciteit van een condensator met diëlektrische constante ε (epsilon) is: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Deze formule is handig voor het berekenen van kleine variabele condensatoren voor radio's.Dezelfde formule kan worden weergegeven als: C = (ε_0 ∙ ε ∙ S) / d, waarbij ε_0 de diëlektrische constante of de diëlektrische constante van het vacuüm is (ε_0 = 8.859 ∙ 10 ^ (- 12) F / m); ε is de diëlektrische constante van het diëlektricum.

In deze formule worden de afmetingen vervangen in meters en wordt de capaciteit verkregen in farads.

Voorbeelden van

1. Wat is de capaciteit van de planeet Aarde, waarvan de straal r = 6378 km is?

Aangezien de capaciteit van een bol met een straal van 1 cm gelijk is aan 1,11 pF, is de capaciteit van de aarde: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (De capaciteit van een bal ter grootte van onze planeet is relatief klein. Kleine elektrolytische condensatoren hebben deze capaciteit).

2. Bepaal de capaciteit van een condensator bestaande uit twee platen met elk een oppervlakte S = 120 cm2.

De platen worden gescheiden door een luchtlaag met een dikte van d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Bepaal de capaciteit van de condensator met de gegevens in het vorige voorbeeld, als de ruimte tussen de platen is gevuld met vetvrij papier met een diëlektrische constante ε = 4, glas (ε = 7), elektrisch karton (ε = 2) , mica (ε = 8 ).

Een waspapiercondensator heeft een capaciteit C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

De capaciteit van een glascondensator is C = 7 ∙ 21,2 = 148,4 pF.

De capaciteit van de kartonnen condensator is C = 2 ∙ 21,2 = 42,3 pF.

De capaciteit van de mica-condensator is C = 8 ∙ 21,2 = 169,6 pF.

4. Wat is de capaciteit van een luchtrotatiecondensator voor een radio-ontvanger bestaande uit 20 platen met een oppervlakte van 20 cm2 als de afstand tussen de platen 0,06 cm is (Fig. 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

De condensator getoond in Fig.3, bestaat uit afzonderlijke eenvoudigste condensatoren met twee platen, waarvan het aantal gelijk is aan n-1.

5. Een papieren condensator met capaciteit C = 2 μF bestaat uit twee stroken aluminiumfolie C en twee stroken van een diëlektricum gemaakt van vetvrij papier B met een diëlektrische constante ε = 6. De dikte van het waspapier is d = 0,1 mm. De gevouwen stroken zijn opgerold, de draden zijn gemaakt van de stalen platen. Bepaal de lengte van de stalen strip van de condensor als deze 4 cm breed is (fig. 4).

Rijst. 4.

Eerst bepalen we de oppervlakte van één strook met de formule C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, vandaar S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2.000.000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

De lengte van elke strook is l = 37680/4 = 9420 cm = 94,2 m.