Elektronen gedragen zich als golven

Natuurkundigen weten al lang dat licht een elektromagnetische golf is. Tot op de dag van vandaag twijfelt niemand aan deze positie, aangezien licht duidelijk alle tekenen van golfgedrag vertoont: lichtgolven kunnen elkaar overlappen, waardoor een interferentiepatroon ontstaat, ze kunnen ook uit elkaar gaan en rond obstakels buigen in de diffractietijd.

Als we een vogel zien die loopt als een eend, zwemt als een eend en kwaakt als een eend, noemen we die vogel een eend. Zo is het licht elektromagnetische golfgebaseerd op objectief waargenomen tekenen van het gedrag van zo'n golf in licht.

Aan het einde van de 19e en 20e eeuw zouden natuurkundigen echter beginnen te praten over het "deeltjesgolf-dualisme" van licht. Het blijkt dat de wetenschap dat licht een elektromagnetische golf is niet alles is wat de wetenschap over licht weet. Wetenschappers hebben een zeer interessante eigenschap in licht ontdekt.

Het blijkt dat licht zich op de een of andere manier manifesteert ALS het gedrag van een stroom deeltjes.Gebleken is dat de door het licht meegevoerde energie, na te zijn geteld over een bepaalde tijdsperiode door een speciale detector, toch blijkt te zijn samengesteld uit losse (hele) stukjes.

Daarom werd het waar dat de energie van licht discreet is, omdat het als het ware is samengesteld uit individuele deeltjes - "quanta", dat wil zeggen uit de kleinste hele delen van energie. Zo'n lichtdeeltje, dat een eenheid (of kwantum) energie draagt, werd een foton genoemd.

De energie van één foton wordt gevonden met de volgende formule:

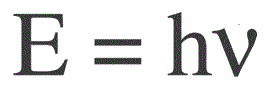
E — fotonenergie, h — de constante van Planck, v — frequentie.

De Duitse natuurkundige Max Planck stelde eerst experimenteel vast dat de lichtgolf discreet is en berekende de waarde van de constante h, die voorkomt in de formule voor het vinden van de energie van individuele fotonen. Deze waarde bleek te zijn: 6.626 * 10-34 J * s. Planck publiceerde de resultaten van zijn werk eind 1900.

Denk bijvoorbeeld aan een paarse straal. De frequentie van dergelijk licht (f of v) is 7,5 * 1014 Hz. De constante van Planck (h) is 6,626 * 10-34 J * s. Dit betekent dat de energie van het foton, (E), karakteristiek voor de kleur violet, 5 * 10-19 J is. Dit is zo'n klein deel van de energie dat het heel moeilijk te vangen is.

Stel je een bergstroom voor - het stroomt als één geheel en het is onmogelijk om met het blote oog te zien dat de stroom eigenlijk uit individuele watermoleculen bestaat. Tegenwoordig weten we echter dat het macroscopische object - stroom - eigenlijk discreet is, dat wil zeggen, het bestaat uit individuele moleculen.

Dit betekent dat als we een moleculenteller naast de stroom kunnen plaatsen om de watermoleculen te tellen die langs de stroom stromen, de detector altijd alleen hele aantallen watermoleculen zal tellen, geen gedeeltelijke.

Evenzo zal de grafiek van de totale energie van het foton E, berekend op tijdstip t — altijd niet lineair blijken te zijn (gele figuur), maar stapsgewijs (groene figuur):

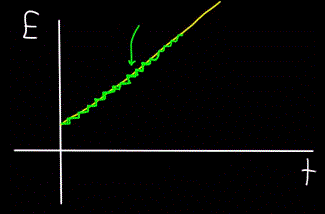
Dus fotonen bewegen, ze dragen energie, daarom hebben ze momentum. Maar een foton heeft geen massa. Hoe kun je dan momentum vinden?

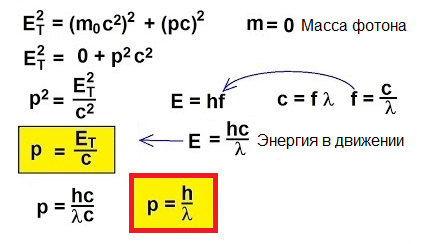
Voor objecten die bewegen met snelheden die dicht bij de lichtsnelheid liggen, is de klassieke formule p = mv simpelweg niet van toepassing. Om te begrijpen hoe we momentum kunnen vinden in dit ongebruikelijke geval, gaan we naar de speciale relativiteitstheorie:

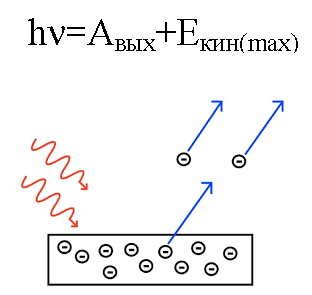
In 1905 verklaarde Albert Einstein vanuit dit standpunt fotoëlektrisch effect… We weten dat de metalen plaat elektronen bevat, die binnenin worden aangetrokken door de positief geladen kernen van de atomen en daardoor in het metaal worden vastgehouden. Maar als je zo'n plaat beschijnt met licht van een BEPAALDE frequentie, dan kun je elektronen uit de plaat slaan.

Het is alsof licht zich gedraagt ​​als een stroom deeltjes met momentum.En hoewel een foton geen massa heeft, interageert het toch op de een of andere manier met een elektron in een metaal, en onder bepaalde omstandigheden kan een foton een elektron uitschakelen.

Dus als een foton dat op de plaat valt voldoende energie heeft, zal het elektron uit het metaal worden geslagen en met snelheid v uit de plaat bewegen. Zo'n uitgeschakeld elektron wordt een foto-elektron genoemd.

Omdat het uitgeschakelde elektron een bekende massa m heeft, zal het een bepaalde kinetische energie mv hebben.

De energie van het foton, wanneer het op het metaal inwerkt, wordt omgezet in de energie van de uitgang van het elektron uit het metaal (werkfunctie) en in de kinetische energie van het elektron, waardoor het uitgeschakelde elektron begint te bewegen uit het metaal en verlaat het.

Stel dat een foton met bekende golflengte het oppervlak van een metaal treft waarvan de uittreefunctie (van een elektron uit het metaal) bekend is. In dit geval kan de kinetische energie van een elektron dat wordt uitgezonden door een bepaald metaal gemakkelijk worden gevonden, evenals de snelheid ervan.

Als de energie van het foton niet voldoende is voor het elektron om de werkfunctie uit te voeren, dan kan het elektron eenvoudigweg het oppervlak van het gegeven metaal niet verlaten en wordt het foto-elektron niet gevormd.

In 1924, een Franse natuurkundige Louis de Broglie een baanbrekend idee naar voren brengen volgens welke niet alleen fotonen van licht, maar ook elektronen zelf kunnen zich als golven gedragen. De wetenschapper heeft zelfs een formule afgeleid voor de hypothetische golflengte van het elektron. Deze golven werden later "de Broglie-golven" genoemd.

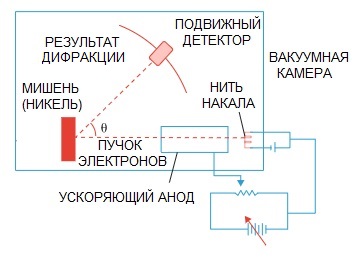
De hypothese van De Broglie werd later bevestigd. Een natuurkundig experiment met elektronendiffractie, uitgevoerd in 1927 door de Amerikaanse wetenschappers Clinton Davison en Lester Germer, wees uiteindelijk op het golfkarakter van het elektron.

Wanneer een elektronenbundel door een speciale atomaire structuur werd geleid, lijkt het erop dat de detector het beeld had moeten opnemen als deeltjes die achter elkaar rondvlogen, wat logischerwijs te verwachten zou zijn als elektronen deeltjes waren.

Maar in de praktijk hebben we een beeldkarakteristiek van golfdiffractie. Bovendien zijn de lengtes van deze golven volledig in overeenstemming met het door de Broglie voorgestelde concept.

Uiteindelijk maakte het idee van De Broglie het mogelijk om het principe van het atoommodel van Bohr uit te leggen, en later maakte het het voor Erwin Schrödinger mogelijk om deze ideeën te generaliseren en de basis te leggen voor de moderne kwantumfysica.