Circuittopologieën: basisconcepten

Een elektrisch circuit is een set apparaten (elementen) en hun verbindingsdraden waardoor een elektrische stroom kan vloeien. Alle elementen van elektrische circuits delen in passief en actief.

Actieve elementen zetten verschillende soorten energie (mechanisch, chemisch, licht, etc.) om in elektrische energie. Bij passieve apparaten wordt elektrische energie omgezet in andere soorten energie. Actieve elementen worden bronnen genoemd, passieve worden consumenten of ontvangers genoemd.

In de circuittheorie worden geïdealiseerde modellen van elektrische elementen overwogen. Dit maakt de beschrijving van de elementen zo eenvoudig mogelijk. Complexere, reële elementen worden gemodelleerd op basis van een reeks geïdealiseerde elementen.

De belangrijkste passieve elementen van elektrische circuits zijn weerstand (resistief element), inductor (inductief element) en condensator (capacitief element). Elementen worden in een elektrisch circuit geïnstalleerd om spanning en stroom van een bepaalde waarde en vorm te genereren (zie — Elektrisch circuit en zijn elementen).

Een elektrisch circuit bestaat uit takken en knopen. Tak — dit is een gedeelte van een elektrisch circuit (circuit) waar dezelfde stroom doorheen vloeit. Een knoop — aansluiting van drie of meer aftakkingen. Op het elektrisch schema wordt het knooppunt aangegeven met een punt (Fig. 1).

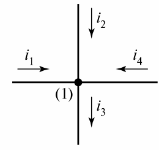
Rijst. 1. Definieer het knooppunt in het diagram

Indien nodig worden de knooppunten van het diagram van links naar rechts van boven naar beneden genummerd.

In afb. 2 toont de resistief-capacitieve tak waarin de stroom iC vloeit.

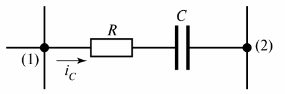
Rijst. 2. Resistief-capacitieve tak

Er kan een andere definitie van een tak worden gegeven: het is een gedeelte van een circuit tussen twee aangrenzende knooppunten (knooppunten (1) en (2) in figuur 2).

Ketting Is er een gesloten pad in het elektrische circuit. Het circuit kan worden gesloten door alle takken, inclusief voorwaardelijke takken waarvan de weerstand gelijk is aan oneindig.

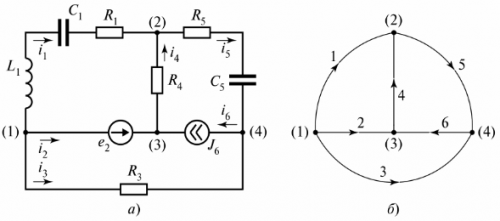
In afb. 3 toont een vertakt elektrisch circuit dat uit drie takken bestaat.

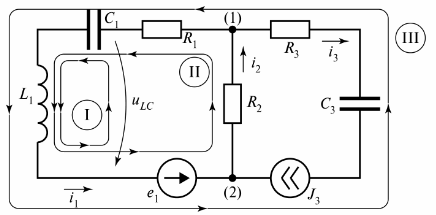
Rijst. 3. Elektrisch circuit met twee circuits

Het diagram toont drie circuits en circuit I is gesloten door een tak van oneindige weerstand. Deze tak wordt aangeduid als spanning tiLC.

Voor de schakeling van Fig. 3 is het mogelijk om vele lussen samen te stellen die worden gesloten door echte of voorwaardelijke vertakkingen, maar voor de berekening van elektrische ruis wordt het concept van «onafhankelijke lus» gebruikt. Het aantal onafhankelijke circuitlussen wordt altijd ingesteld als het minimum dat nodig is voor de berekening.

Onafhankelijke circuits zijn altijd gesloten, maar vertakkingen die een weerstand hebben die niet gelijk is aan oneindig, en elk onafhankelijk circuit bevat ten minste één vertakking die niet is opgenomen in andere circuits. Voor complexe elektrische circuits kunt u het aantal onafhankelijke circuits bepalen met behulp van het schakelschema.

Op het schakelschema een voorwaardelijke weergave van het circuit wordt aangeroepen, waarin elke tak wordt vervangen door een lijnstuk. Items in filialen worden niet weergegeven. In FIG. 4 toont een aftakschakeling en zijn schema.

Rijst. 4. Vertakt elektrisch circuit: a - schakelschema, b - schema

Om een ​​diagram van een diagram te maken, moet u de knooppunten verbinden met zijlijnen zonder er elementen op te specificeren. De takken zijn genummerd en de richtingen van de stromingen erop worden aangegeven met pijlen. De grafiek zelf heeft geen fysieke betekenis, maar kan worden gebruikt om het aantal en het type onafhankelijke contouren te bepalen. Voor dit doel wordt een "grafische boom" opgesteld.

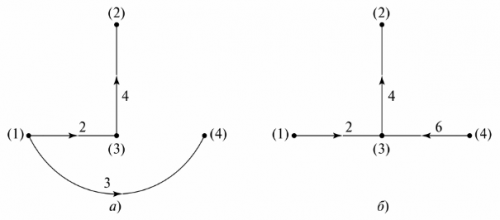
Grafische boom Het vertegenwoordigt de grafiek van een circuit waarvan de knooppunten zodanig zijn verbonden door takken dat er geen gesloten lus ontstaat. Er kunnen verschillende opties zijn om een ​​grafische boom weer te geven. In afb. 5 toont twee mogelijke opties voor de schakeling van Fig. 4.

Rijst. 5. Grafische boomstructuur van het schema

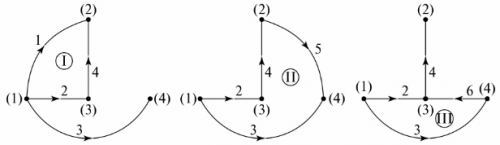
Het aantal ontbrekende takken in de grafiekboom is gelijk aan het aantal onafhankelijke lussen van het circuit. In het voorbeeld zijn dit drie takken, drie onafhankelijke lussen. De configuratie van onafhankelijke lussen kan worden verkregen door achtereenvolgens de knooppunten van de grafenboom te verbinden met takken die niet gespecificeerd zijn in de grafenboom. Voor de grafiekboom in Fig. 5, en de onafhankelijke contouren worden getoond in Fig. 6.

Rijst. 6. Zelfstandige contouren bepalen via de grafenboom

De selectie van een optie om onafhankelijke circuits te configureren voor het berekenen van het circuit wordt uitgevoerd tijdens circuitanalyse. U moet dergelijke contouren kiezen zodat de berekening zo eenvoudig mogelijk is, d.w.z. het aantal afhankelijke vergelijkingen in het systeem is minimaal.

Topologische vergelijkingen leggen een relatie vast tussen spanningen en stromen in een circuit, en het aantal en type vergelijkingen hangt niet af van welke elementen in de takken zijn opgenomen. Topologische vergelijkingen omvatten vergelijkingen die zijn samengesteld uit volgens de wetten van Kirchhoff.