Driefasige netvoeding: actief, reactief, vol
De waarden van het totale actieve en totale blindvermogen van het driefasencircuit zijn gelijk aan de som van het actieve en blindvermogen voor elk van de drie fasen A, B en C. Deze verklaring wordt geïllustreerd door het volgende formules:
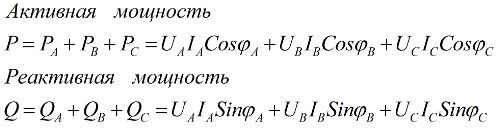
hier zijn Ua, Ub, Uc, Ia, Ib, Ic de waarden van fasespanningen en stromen en φ is de faseverschuiving.
Wanneer de belasting symmetrisch is, dat wil zeggen, in omstandigheden waarin het actieve en reactieve vermogen van elk van de fasen gelijk is aan elkaar, om het totale vermogen van het meerfasencircuit te vinden, volstaat het om de waarde van het fasevermogen te vermenigvuldigen met het aantal betrokken fasen. Het totale vermogen wordt bepaald op basis van de verkregen waarden van de actieve en reactieve componenten:
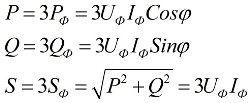
In de bovenstaande formules kunnen de fasewaarden van de grootheden worden uitgedrukt in termen van hun lineaire waarden, die zullen verschillen voor ster- of delta-verbindingsschema's voor gebruikers, maar de vermogensformules zullen uiteindelijk hetzelfde zijn:
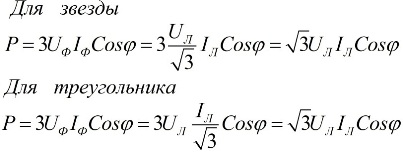
Uit de bovenstaande uitdrukkingen volgt dat ongeacht het verbindingsschema van de ontvangers van elektrische energie, of het nu een driehoek of een ster is, als de belasting symmetrisch is, de formules voor het vinden van het vermogen dezelfde vorm zullen hebben, zowel voor een driehoek en voor een ster:
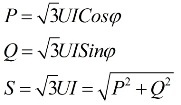
Deze formules tonen lineaire waarden van spanning en stroom en zijn geschreven zonder subscripts. Meestal wordt zo'n notatie gevonden, zonder subscripts, dat wil zeggen, als er geen subscripts zijn, dan bedoelen we lineaire waarden.
Een speciaal meetapparaat, genaamd wattmeter… De meetwaarden worden bepaald door de formule:
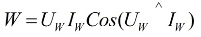
in de bovenstaande formule zijn Uw en Iw de vectoren van de spanning die op de belasting wordt toegepast en de stroom die er doorheen vloeit.
De aard van de actieve belasting en het faseaansluitschema kunnen verschillen, daarom zullen, afhankelijk van de specifieke omstandigheden, de aansluitschema's van de wattmeter verschillen.
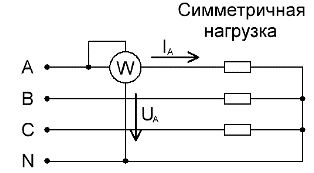
Voor symmetrisch belaste driefasige circuits is voor een ruwe meting van het totale actieve vermogen, indien geen hoge nauwkeurigheid vereist is, één wattmeter aangesloten op slechts één van de fasen voldoende. Daarna, om de waarde van het actieve vermogen van het hele circuit te krijgen, blijft het om de meetwaarden van de wattmeter te vermenigvuldigen met het aantal fasen:
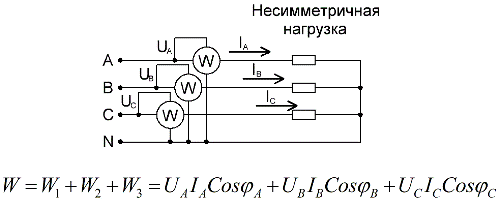
Voor een vierdraads circuit met een neutrale draad, om het actieve vermogen nauwkeurig te meten, zijn drie wattmeters nodig, die elk worden gelezen en vervolgens opgeteld om een waarde te verkrijgen voor het totale vermogen van het circuit:
Als er geen nulleider in een driefasig circuit zit, zijn twee wattmeters voldoende om het totale vermogen te meten, zelfs als de belasting onevenwichtig is.
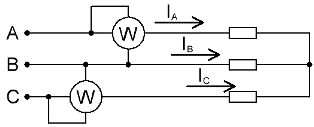
Bij afwezigheid van een nulleider zijn de fasestromen onderling verbonden volgens de eerste wet van Kirchhoff:
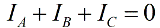
Dan is de som van de meetwaarden van een paar wattmeters gelijk aan:
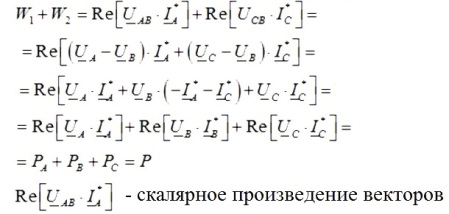
Dus als je de waarden van een paar wattmeters optelt, krijg je het totale actieve vermogen in het driefasige circuit dat wordt bestudeerd, en de waarden van de wattmeters zijn afhankelijk van zowel de grootte van de belasting als de aard ervan.
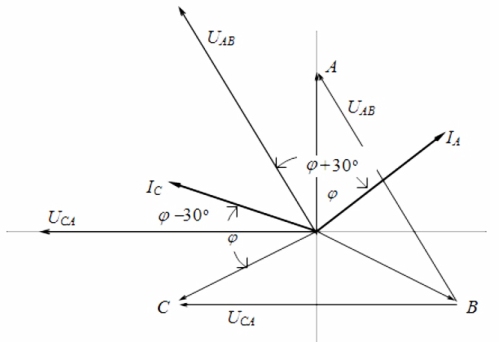
Kijkend naar het vectordiagram van stromen en spanningen in verband met een symmetrische belasting, kan worden geconcludeerd dat de aflezingen van wattmeters worden bepaald door de volgende formules:
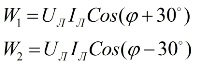
Na analyse van deze uitdrukkingen kan worden begrepen dat bij een puur actieve belasting, wanneer φ = 0, de aflezingen van de twee wattmeters aan elkaar gelijk zullen zijn, dat wil zeggen W1 = W2.
Met actieve belastingsinductantie, wanneer 0 ≤ φ ≤ 90 °, zullen de waarden van wattmeter 1 lager zijn dan die van wattmeter 2, dat wil zeggen W1 60 °, de waarden van wattmeter 1 zullen negatief zijn, dat wil zeggen W1 <0.
Met een actief-capacitieve aard van de belasting, wanneer 0 ≥ φ≥ -90 °, zullen de meetwaarden van wattmeter 2 kleiner zijn dan die van wattmeter 1, dat wil zeggen W1> W2. Bij φ <-60 ° worden de uitlezingen van wattmeter 2 negatief.
