Bronnen van harmonischen in elektrische netwerken
Aangezien niet-lineaire elementen altijd aanwezig zijn in moderne elektrische apparaten, vooral in industriële netwerken, worden stroomcurven en spanningscurven daardoor vervormd en verschijnen er hogere harmonischen in netwerken.
Allereerst is niet-sinusoïdaliteit te wijten aan de aanwezigheid van statische omvormers, vervolgens - synchrone generatoren, lasmachines, fluorescentielampen, boogovens, transformatoren, motoren en andere niet-lineaire belastingen.
Wiskundig gezien kan de niet-sinusoïditeit van de stroom- en spanningscurven worden weergegeven als de som van de hoofdharmonische van de netfrequentie en de hogere harmonischen die daarvan een veelvoud zijn. Harmonische analyse resulteert in een trigonometrische Fourier-reeks en de waarden van frequenties en fasen van de resulterende harmonischen kunnen eenvoudig worden berekend met behulp van de formule:

In feite kan de resulterende combinatie van niet-sinusvormige spanningen en stromen in een driefasig netwerk asymmetrisch of symmetrisch zijn.Een symmetrisch systeem van niet-sinusvormige spanningen voor veelvouden van drie harmonischen (k = 3n) leidt tot de vorming van een systeem van spanningen met een nulsequentie.
Bovendien genereert de harmonische in het driefasennetwerk bij k = 3n + 1 een symmetrisch systeem van negatieve sequentiespanningen. Dus elke k-harmonische van een symmetrisch systeem van niet-sinusvormige spanningen resulteert in een symmetrisch systeem van fasespanningen van directe, omgekeerde of nulsequentie.
In de praktijk blijkt het stelsel van niet-sinusvormige fasespanningen echter asymmetrisch te zijn. Dus, magnetische kernen van driefasige transformatoren zelf zijn ze niet-lineair en asymmetrisch, aangezien de lengtes van de magnetische paden voor de midden- en eindfase een factor 1,9 verschillen. Hierdoor zijn de effectieve waarden van de magnetiserende stromen van de middenfase 1,3 - 1,55 keer kleiner dan de waarden van de magnetiserende stromen van de laatste fasen.
Asymmetrische harmonischen worden ontleed in symmetrische componenten wanneer elke k-harmonische een asymmetrisch systeem van fasespanningen vormt en typisch componenten bevat van drie reeksen: nul, voorwaarts en achterwaarts.
Driefasige netwerken met een geïsoleerde nulleider worden gekenmerkt door de afwezigheid van nulsequentiecomponenten in elk van de fasen, op voorwaarde dat er geen aardfouten zijn. Als gevolg hiervan zijn er geen veelvouden van drie harmonischen in de fasestromen, maar zijn er andere harmonischen die omgekeerde en positieve sequentiecomponenten bevatten.
Vermogensgelijkrichters hebben in de regel aan de DC-zijde grote inductanties, dit zijn DC-machinewikkelingen en afvlakspoelen.Deze inductanties zijn vele malen hoger dan de equivalente inductantie van de wisselstroomzijde, daarom gedragen dergelijke gelijkrichters zich ten opzichte van het wisselstroomnetwerk als bronnen van hogere harmonische stroom. De stroom die met een harmonische frequentie naar het netwerk wordt geleid, heeft een waarde die niet afhankelijk is van de parameters van het voedingsnetwerk.
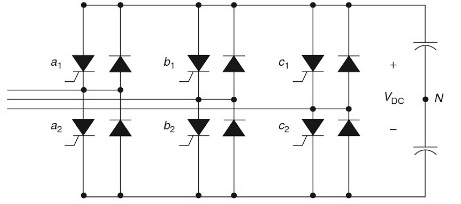
Voor driefasige elektrische netwerken is het kenmerkend om driefasige dubbelfasige gelijkrichters voor 6 kleppen als dergelijke omvormers te gebruiken, van waaruit ze zespuls of zesfasig worden genoemd. De stroomcurve voor elk van de fasen kan in dit geval worden beschreven door de vergelijking (voor de stroom van één fase A):
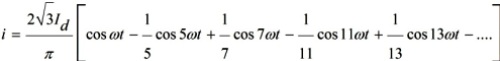
Het is te zien dat de fasestromen alleen oneven harmonischen bevatten die geen veelvouden van drie zijn, en de tekens van deze harmonischen wisselen elkaar af: positieve harmonischen van de 6k + 1e orde en negatieve harmonischen van de 6k-1e orde.
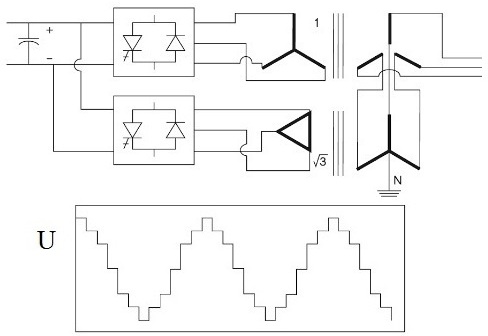
Als een twaalffasige gelijkrichter wordt gebruikt, wanneer een paar zesfasige gelijkrichters is aangesloten op een paar driefasige transformatoren (de secundaire spanningen zijn in fase verschoven met pi / 6), dan harmonischen van 12k + 1 en 12k- 1-orders verschijnen respectievelijk.
Voordat gelijkrichters werden gebruikt, waren alleen transformatoren en verschillende elektrische machines de belangrijkste bron van hogere harmonischen in elektrische netwerken. Maar zelfs vandaag de dag zijn transformatoren de meest voorkomende elementen van elektrische netwerken.
De reden waarom transformatoren hogere harmonischen genereren, is de niet-lineaire magnetisatiecurve van de magnetische circuits en de constante aanwezigheid van hysteresis loops… Een niet-lineaire magnetiseringscurve en hysteresislus genereren vervormingen van de oorspronkelijke sinusvormige magnetiseringsstroom zonder belasting en het resultaat is hogere harmonischen in de stroom die de transformator van het net trekt.
Transformatoren van de 110 kV-klasse hebben niet meer dan 1% nullaststroom en transformatoren van de 6-10 kV-klasse - niet meer dan 2-3%. Dit zijn kleine stromen en hun actieve verliezen in het magnetische circuit zijn verwaarloosbaar. Het is de magnetisatiecurve die ertoe doet, niet de hysteresislus.
De magnetisatiecurve is symmetrisch en er zijn zelfs geen harmonischen in de uitbreiding van de Fourier-reeks. De vervorming van de magnetiserende stroom wordt veroorzaakt door oneven harmonischen, waaronder veelvouden van drie. De derde harmonische is bijzonder uitgesproken, maar de vijfde en zevende harmonische zijn ook het meest significant.
EMF-harmonischen en stroomharmonischen zijn ook kenmerkend voor motoren, zowel synchroon als asynchroon… Deze harmonischen worden veroorzaakt door dezelfde fenomenen als stroomharmonischen die worden gegenereerd door transformatoren: de niet-lineariteit van de magnetisatiecurve van de materialen waaruit de stator en rotor zijn gemaakt.
Het frequentiespectrum van stroomharmonischen van elektromotoren, zoals dat van transformatoren, omvat oneven harmonischen, waaronder duidelijk veelvouden van drie. De belangrijkste hier zijn de 3e, 5e en 7e harmonischen.
Net als in het geval van transformatoren, stellen ruwe berekeningen ons in staat om het percentage van stromen van de 3e, 5e en 7e harmonische op 40% te nemen voor de derde harmonische, 30% voor de vijfde harmonische en 20% voor de zevende harmonische (percentage van de ruststroom).
