Verliezen en spanningsdalingen - wat zijn de verschillen

In het gewone menselijke leven worden de woorden "verlies" en "val" gebruikt om het feit van een afname van bepaalde prestaties aan te duiden, maar ze betekenen een andere waarde.

In dit geval betekent «verliezen» verlies van een onderdeel, schade, verkleining van het eerder bereikte niveau. Verliezen zijn ongewenst, maar u kunt ze tolereren.

Het woord "vallen" wordt opgevat als een ernstiger nadeel dat gepaard gaat met een volledige ontneming van rechten. Zo kunnen zelfs incidenteel optredende verliezen (bijvoorbeeld een portefeuille) in de loop van de tijd leiden tot een daling (bijvoorbeeld het niveau van de materiële levensduur).

In dit verband zullen we deze vraag beschouwen in relatie tot de spanning van het elektrische netwerk.

Hoe verliezen en spanningsvallen worden gevormd

Elektriciteit wordt over lange afstanden vervoerd door bovengrondse lijnen van het ene onderstation naar het andere.

Bovenleidingen zijn ontworpen om het toegestane vermogen over te brengen en zijn gemaakt van metalen draden van een bepaald materiaal en doorsnede. Ze creëren een resistieve belasting met een weerstandswaarde van R en een reactieve belasting van X.

Aan de ontvangende kant staat het transformatorelektriciteits conversie.De spoelen hebben een actieve en uitgesproken inductieve weerstand XL. De secundaire zijde van de transformator verlaagt de spanning en geeft deze verder door aan de verbruikers, wiens belasting wordt uitgedrukt door de waarde van Z en is actief, capacitief en inductief van aard. Dit heeft ook invloed op de elektrische parameters van het netwerk.

De spanning die wordt toegepast op de draden van de ondersteuning van de bovenleiding, die zich het dichtst bij het onderstation voor krachtoverbrenging bevindt, overwint de reactieve en actieve weerstand van het circuit in elke fase en creëert er een stroom in, waarvan de vector afwijkt van de vector van de aangelegde spanning over een hoek φ.

De aard van de verdeling van spanningen en de stroom van stromen langs de lijn voor een symmetrische belastingsmodus wordt getoond op de foto.

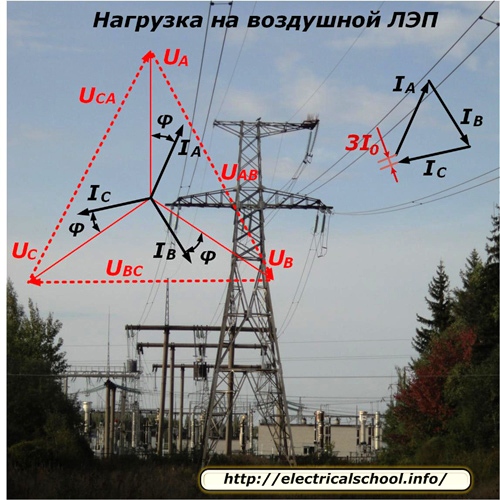
Aangezien elke fase van de lijn een ander aantal consumenten voedt die ook willekeurig zijn losgekoppeld of verbonden met het werk, is het technisch erg moeilijk om de fasebelasting perfect in evenwicht te brengen. Er zit altijd een onbalans in, die wordt bepaald door de vectoroptelling van de fasestromen en geschreven als 3I0. In de meeste berekeningen wordt het simpelweg genegeerd.

De energie die door het verzendende onderstation wordt verbruikt, wordt gedeeltelijk besteed aan het overwinnen van de weerstand van de lijn en bereikt de ontvangende kant met weinig verandering. Deze fractie wordt gekenmerkt door verlies en spanningsval, waarvan de vector iets in amplitude afneemt en in elke fase een hoek verschuift.

Hoe verliezen en spanningsverlies worden berekend

Om de processen die plaatsvinden tijdens de transmissie van elektriciteit te begrijpen, is de vectorvorm handig om de belangrijkste kenmerken weer te geven. Ook verschillende wiskundige rekenmethoden zijn op deze methode gebaseerd.

Om de berekeningen te vereenvoudigen driefasig systeem het wordt vertegenwoordigd door drie enkelfasige equivalente circuits. Deze methode werkt goed met een symmetrische belasting en stelt u in staat om de processen te analyseren wanneer deze is verbroken.

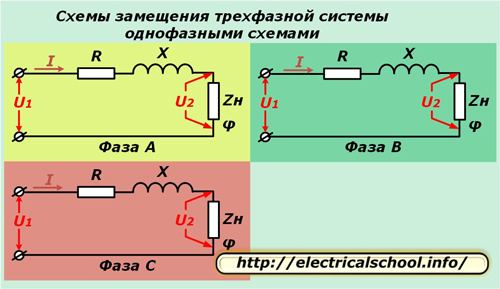
In de bovenstaande diagrammen zijn de actieve R en reactantie X van elke geleider van de lijn in serie geschakeld met de complexe belastingsweerstand Zn gekenmerkt door de hoek φ.

Bovendien wordt de berekening van spanningsverlies en spanningsval in één fase uitgevoerd. Om dit te doen, moet u de gegevens specificeren. Hiervoor wordt een onderstation geselecteerd dat energie ontvangt, waarbij de toegestane belasting al moet worden bepaald.

De spanningswaarde van elk hoogspanningssysteem is al aangegeven in de naslagwerken en de weerstanden van de draden worden bepaald door hun lengte, doorsnede, materiaal en configuratie van het netwerk. De maximale stroom in het circuit wordt ingesteld en beperkt door de eigenschappen van de draden.

Daarom hebben we om de berekeningen te starten: U2, R, X, Z, I, φ.

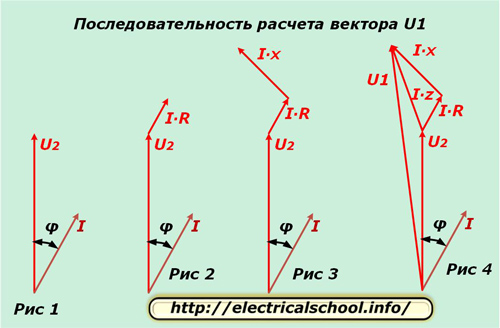
We nemen één fase, bijvoorbeeld «A» en scheiden ervoor in het complexe vlak de vectoren U2 en I, verplaatst over een hoek φ, zoals weergegeven in figuur 1. Het potentiaalverschil in de actieve weerstand van de geleider valt samen in richting met de stroom en de grootte wordt bepaald uit de uitdrukking I ∙ R. We stellen deze vector uit vanaf het einde van U2 (Fig. 2).

Het potentiaalverschil in de reactantie van de geleider verschilt van de richting van de stroom met een hoek φ1 en wordt berekend uit het product I ∙ X. We stellen het uit van de vector I ∙ R (Fig. 3).

Ter herinnering: voor de positieve draairichting van de vectoren in het complexe vlak wordt de beweging tegen de klok in genomen. De stroom die door de inductieve belasting vloeit loopt een hoek achter op de aangelegde spanning.

Figuur 4 toont het uitzetten van de potentiaalverschilvectoren op de totale draadweerstand I ∙ Z en de spanning aan de ingang van de schakeling U1.

Nu kunt u de invoervectoren vergelijken met het equivalente circuit en over de belasting. Om dit te doen, plaatst u het resulterende diagram horizontaal (Fig. 5) en tekent u een boog vanaf het begin met de straal van de module U1 totdat deze de richting van de vector U2 snijdt (Fig. 6).

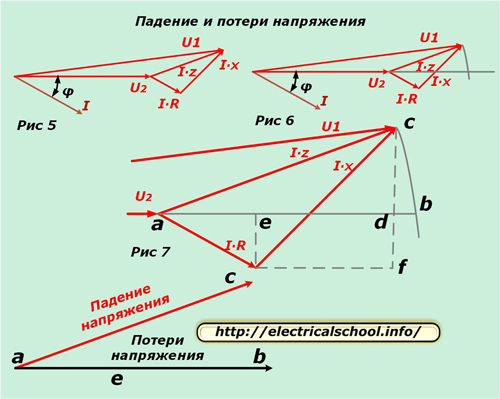
Figuur 7 toont een vergroting van de driehoek voor meer duidelijkheid en het tekenen van hulplijnen, die de kenmerkende snijpunten aangeven met letters.

Onderaan de afbeelding is te zien dat de resulterende vector ac de spanningsval wordt genoemd en ab het verlies. Ze verschillen in grootte en richting. Als we terugkeren naar de oorspronkelijke schaal, zullen we zien dat ac wordt verkregen als resultaat van geometrische aftrekking van vectoren (U2 van U1), en ab is rekenkunde. Dit proces wordt weergegeven in de onderstaande afbeelding (Fig. 8).

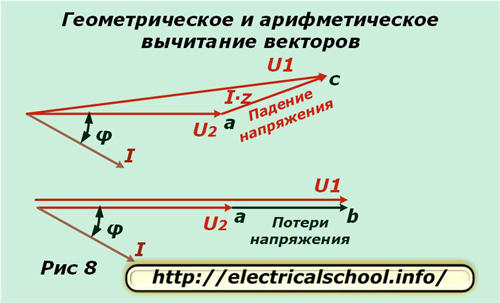
Afleiding van formules voor het berekenen van spanningsverliezen

Laten we nu teruggaan naar figuur 7 en zien dat het bd-segment erg klein is. Om deze reden wordt het verwaarloosd in de berekeningen en wordt het spanningsverlies berekend uit de segmentlengte ad. Het bestaat uit twee lijnstukken ae en ed.

Aangezien ae = I ∙ R ∙ cosφ en ed = I ∙ x ∙ sinφ, kan het spanningsverlies voor één fase worden berekend met de formule:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Als we aannemen dat de belasting in alle fasen symmetrisch is (voorwaardelijk verwaarlozen van 3I0), kunnen we wiskundige methoden gebruiken om het spanningsverlies in de lijn te berekenen.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Als de rechterkant van deze formule wordt vermenigvuldigd en gedeeld door de netwerkspanning Un, dan krijgen we een formule waarmee we pBerekening van spanningsverliezen door de voeding kunnen uitvoeren.

∆Ul = (P ∙ r + Q ∙ x) / Un

De waarden van actief P en reactief Q-vermogen kunnen worden ontleend aan lijnmeterstanden.

Het spanningsverlies in een elektrisch circuit hangt dus af van:

• actief en reactantie van het circuit;

• componenten van toegepast vermogen;

• de grootte van de aangelegde spanning.

Afleiding van formules voor het berekenen van de dwarscomponent van de spanningsval

Laten we teruggaan naar figuur 7. De waarde van de vector ac kan worden weergegeven door de schuine zijde van een rechthoekige driehoek acd. We hebben de advertentievoet al berekend. Laten we de transversale component cd bepalen.

De figuur laat zien dat cd = cf-df.

df = ce = I ∙ R ∙ zonde φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Met behulp van de verkregen modellen voeren we kleine wiskundige transformaties uit en verkrijgen we de transversale component van de spanningsval.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Bepaling van de formule voor het berekenen van de spanning U1 aan het begin van de hoogspanningslijn

Als we de waarde kennen van de spanning aan het einde van de lijn U2, het verlies ∆Ul en de transversale component van de daling δU, kunnen we de waarde van de vector U1 berekenen met de stelling van Pythagoras. In uitgebreide vorm heeft het de volgende vorm.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Praktisch gebruik

De berekening van spanningsverliezen wordt uitgevoerd door ingenieurs in het stadium van het creëren van een elektrisch circuitproject voor de optimale selectie van de configuratie van het netwerk en de samenstellende elementen ervan.

Tijdens de werking van elektrische installaties kunnen, indien nodig, periodiek gelijktijdige metingen van de spanningsvectoren aan de uiteinden van de lijnen worden uitgevoerd en kunnen de resultaten die worden verkregen door de methode van eenvoudige berekeningen worden vergeleken.Deze methode is geschikt voor apparaten die zijn toegenomen eisen vanwege de behoefte aan hoge werknauwkeurigheid.

Spanningsverliezen in secundaire circuits

Een voorbeeld zijn de secundaire circuits van meetspanningstransformatoren, die soms honderden meters lang zijn en worden overgedragen via een speciale voedingskabel met een grotere doorsnede.

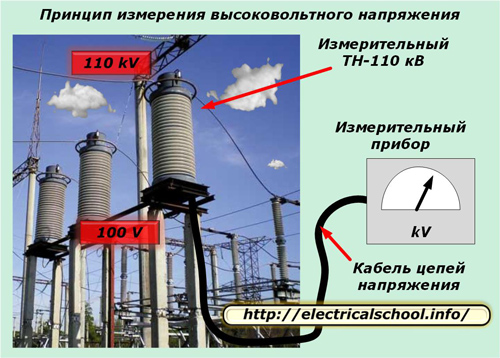
De elektrische eigenschappen van een dergelijke kabel zijn onderhevig aan verhoogde eisen voor de kwaliteit van de spanningsoverdracht.

Moderne beveiliging van elektrische apparatuur vereist de werking van meetsystemen met hoge metrologische indicatoren en een nauwkeurigheidsklasse van 0,5 of zelfs 0,2. Daarom moeten de verliezen van de spanning die erop wordt toegepast, worden bewaakt en in aanmerking worden genomen. Anders kan de door hen geïntroduceerde fout in de werking van de apparatuur alle operationele kenmerken aanzienlijk beïnvloeden.

Spanningsverliezen in lange kabellijnen

Het kenmerk van het ontwerp van de lange kabel is dat deze een capacitieve weerstand heeft vanwege de vrij dichte plaatsing van geleidende kernen en een dunne laag isolatie daartussen. Het buigt verder de stroomvector af die door de kabel gaat en verandert de grootte ervan.

Het effect van spanningsval op capacitieve weerstand moet in aanmerking worden genomen bij de berekening om de waarde van I ∙ z te veranderen. Anders verandert de hierboven beschreven technologie niet.

Het artikel geeft voorbeelden van verliezen en spanningsvallen op bovengrondse hoogspanningslijnen en kabels. Ze zijn echter te vinden in alle elektriciteitsverbruikers, inclusief elektromotoren, transformatoren, inductoren, condensatorbanken en andere apparaten.

De hoeveelheid spanningsverliezen voor elk type elektrische apparatuur is wettelijk geregeld in termen van bedrijfsomstandigheden en het principe van hun bepaling in alle elektrische circuits is hetzelfde.