Een elektron in een elektrisch veld

De beweging van een elektron in een elektrisch veld is een van de belangrijkste fysische processen voor elektrotechniek. figuur Laten we eens kijken hoe dit gebeurt in een vacuüm. Laten we eerst een voorbeeld bekijken van de beweging van een elektron van de kathode naar de anode in een uniform elektrisch veld.

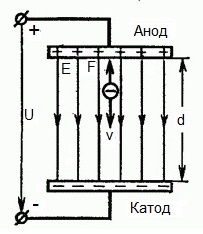
Onderstaande figuur geeft een situatie weer waarin elektron verlaat de negatieve elektrode (kathode) met een verwaarloosbaar kleine beginsnelheid (neigend naar nul) en komt binnen in een uniform elektrisch veldaanwezig tussen twee elektroden.

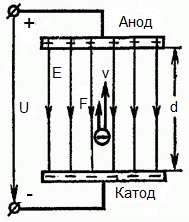
Op de elektroden wordt een constante spanning U aangelegd en het elektrische veld heeft een overeenkomstige sterkte E. De afstand tussen de elektroden is gelijk aan d. In dit geval zal vanaf de kant van het veld een kracht F op het elektron werken, die evenredig is met de lading van het elektron en de sterkte van het veld:

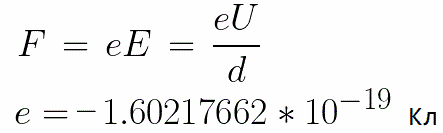
Aangezien het elektron een negatieve lading heeft, zal deze kracht gericht zijn tegen de veldsterktevector E. Dienovereenkomstig zal het elektron in die richting worden versneld door het elektrische veld.

De versnelling ervaren door het elektron is evenredig met de grootte van de kracht F die erop werkt en omgekeerd evenredig met de massa m van het elektron.Aangezien het veld uniform is, kan de versnelling voor een bepaald beeld worden uitgedrukt als:

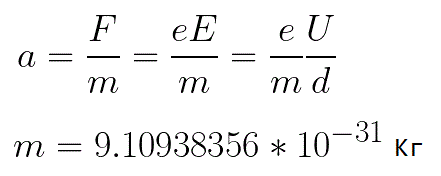
In deze formule is de verhouding van de lading van het elektron tot zijn massa de specifieke lading van het elektron, een grootheid die een fysieke constante is:

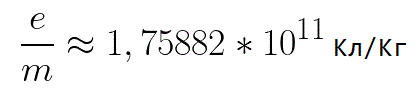
Het elektron bevindt zich dus in een versnellend elektrisch veld omdat de richting van de beginsnelheid v0 samenvalt met de richting van de kracht F aan de kant van het veld en daarom beweegt het elektron gelijkmatig. Als er geen obstakels zijn, zal het het pad d tussen de elektroden afleggen en de anode (positieve elektrode) bereiken met een bepaalde snelheid v. Op het moment dat het elektron de anode bereikt, zal zijn kinetische energie dienovereenkomstig gelijk zijn aan:

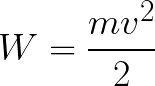
Aangezien het elektron langs het gehele pad d wordt versneld door de krachten van het elektrische veld, verkrijgt het deze kinetische energie als resultaat van het werk dat wordt verricht door de kracht die aan de kant van het veld werkt. Dit werk is gelijk aan:

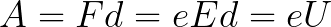
Dan kan de kinetische energie die wordt verkregen door het elektron dat in het veld beweegt, als volgt worden gevonden:

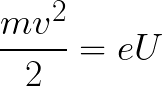
Dat wil zeggen, het is niets meer dan het werk van veldkrachten om een ​​elektron te versnellen tussen punten met een potentiaalverschil U.

Om in dergelijke situaties de energie van een elektron uit te drukken, is het handig om een ​​meeteenheid te gebruiken als de "elektronenvolt", die gelijk is aan de energie van een elektron bij een spanning van 1 volt. En aangezien de elektronenlading constant is, is 1 elektrovolt ook een constante waarde:

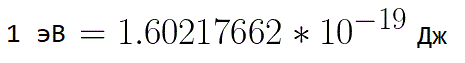
Uit de vorige formule kun je eenvoudig de snelheid van het elektron op elk punt op zijn pad bepalen wanneer het zich in een versnellend elektrisch veld beweegt, waarbij je alleen het potentiaalverschil kent dat het passeerde bij het versnellen:

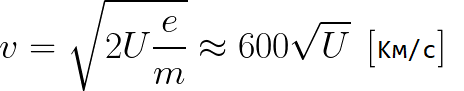
Zoals we kunnen zien, hangt de snelheid van een elektron in een versnellend veld alleen af ​​van het potentiaalverschil U tussen het eindpunt en het beginpunt van zijn pad.

Stel je voor dat het elektron met een verwaarloosbare snelheid van de kathode weg begint te bewegen, en de spanning tussen de kathode en de anode is 400 volt. In dit geval, op het moment dat de anode wordt bereikt, is de snelheid gelijk aan:

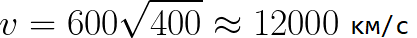
Het is ook gemakkelijk om de tijd te bepalen die het elektron nodig heeft om de afstand d tussen de elektroden af ​​te leggen. Met een gelijkmatig versnelde beweging vanuit rust, blijkt de gemiddelde snelheid de helft van de uiteindelijke snelheid te zijn, dan is de tijd van versnelde vlucht in een elektrisch veld gelijk aan:

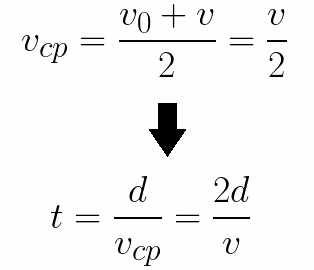
Laten we nu eens kijken naar een voorbeeld waarin een elektron beweegt in een vertragend uniform elektrisch veld, dat wil zeggen, het veld is gericht zoals eerder, maar het elektron begint in de tegenovergestelde richting te bewegen - van de anode naar de kathode.

Stel dat het elektron met een beginsnelheid v de anode verliet en aanvankelijk in de richting van de kathode begon te bewegen. In dit geval zal de kracht F die vanaf de kant van het elektrische veld op het elektron werkt, gericht zijn tegen de elektrische intensiteitsvector E - van de kathode naar de anode.

Het zal de beginsnelheid van het elektron beginnen te verminderen, dat wil zeggen, het veld zal het elektron vertragen. Dit betekent dat het elektron onder deze omstandigheden gelijkmatig en gelijkmatig langzaam zal gaan bewegen. De situatie wordt als volgt beschreven: "een elektron beweegt in een vertragend elektrisch veld."

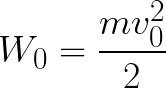
Vanaf de anode begon het elektron te bewegen met niet-nul kinetische energie, die begint af te nemen tijdens de vertraging, aangezien de energie nu wordt verbruikt om de kracht te overwinnen die vanuit het veld op het elektron werkt.

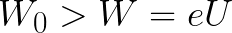
Als de initiële kinetische energie van het elektron bij het verlaten van de anode onmiddellijk groter was dan de energie die door het veld moet worden verbruikt om het elektron te versnellen bij het verplaatsen van de kathode naar de anode (zoals in het eerste voorbeeld), dan zou het elektron een afstand d afleggen en ondanks remmen uiteindelijk de kathode bereiken.

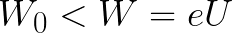
Als de initiële kinetische energie van het elektron kleiner is dan deze kritische waarde, zal het elektron de kathode niet bereiken. Op een gegeven moment stopt het en begint dan een gelijkmatig versnelde beweging terug naar de anode. Als gevolg hiervan zal het veld de energie teruggeven die werd besteed aan het stopproces.

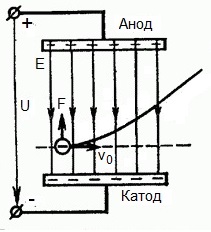
Maar wat als een elektron met snelheid v0 in het actiegebied van een elektrisch veld in een rechte hoek vliegt? Het is duidelijk dat de kracht aan de kant van het veld in dit gebied voor het elektron van de kathode naar de anode is gericht, dat wil zeggen tegen de elektrische veldsterktevector E.

Dit betekent dat het elektron nu twee bewegingscomponenten heeft: de eerste - met een snelheid v0 loodrecht op het veld, de tweede - gelijkmatig versneld onder invloed van de kracht van de kant van het veld gericht naar de anode.

Het blijkt dat het elektron, nadat het in het actieveld is gevlogen, langs een parabolisch traject beweegt. Maar nadat het uit het actiegebied van het veld is gevlogen, zal het elektron zijn uniforme beweging voortzetten door traagheid langs een rechtlijnig traject.