Wat is een elektrische voeding?

De moderne mens komt constant elektriciteit tegen in het dagelijks leven en op het werk, gebruikt apparaten die elektrische stroom verbruiken en apparaten die deze opwekken. Wanneer u met hen werkt, moet u altijd rekening houden met hun capaciteiten die inherent zijn aan de technische kenmerken.

Een van de belangrijkste indicatoren van elk elektrisch apparaat is zo'n fysieke grootheid als elektrische energie... Het is gebruikelijk om de intensiteit of snelheid van opwekking, transmissie of omzetting van elektriciteit in andere soorten energie te noemen, bijvoorbeeld warmte, licht, mechanisch.

Het transport of de overdracht van grote elektrische energie voor industriële doeleinden wordt uitgevoerd volgens hoogspanningsleidingen.

Transformatie elektrische energie wordt uitgevoerd op transformatorstations.

Elektriciteitsverbruik vindt plaats in huishoudelijke en industriële apparaten voor verschillende doeleinden. Een van hun veel voorkomende typen zijn gloeilampen van verschillende classificaties.

Het elektrische vermogen van generatoren, hoogspanningsleidingen en verbruikers in gelijkstroom- en wisselstroomcircuits heeft dezelfde fysieke betekenis, die gelijktijdig wordt uitgedrukt in verschillende verhoudingen, afhankelijk van de vorm van de samengestelde signalen. Om de algemene patronen te definiëren, noties van momentane waarden... Ze benadrukken opnieuw de afhankelijkheid van de transformatiesnelheid van elektriciteit op tijd.

Bepaling van het momentane elektrische vermogen

Om de basisrelaties tussen stroom, spanning en vermogen af ​​te leiden, worden in de theoretische elektrotechniek hun afbeeldingen in de vorm van momentane waarden, die op een bepaald tijdstip zijn vastgelegd, gebruikt.

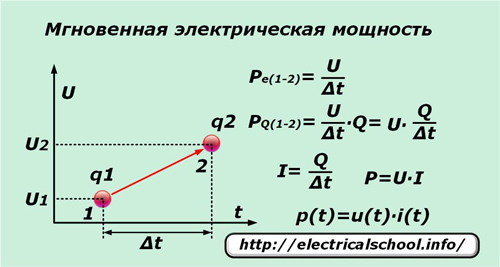
Als in zeer korte tijd ∆t een enkele elementaire lading q onder invloed van spanning U van punt «1» naar punt «2» beweegt, dan verricht deze arbeid gelijk aan het potentiaalverschil tussen deze punten. Door het te delen door het tijdsinterval ∆t, krijgen we de uitdrukking voor het momentane vermogen per eenheid lading Pe (1-2).

Aangezien niet alleen de enkele lading beweegt onder invloed van de aangelegde spanning, maar ook alle aangrenzende ladingen die onder invloed van deze kracht staan, waarvan het aantal handig wordt weergegeven door het getal Q, dan is de momentane waarde van het vermogen PQ (1-2) kan voor hen worden geschreven.

Na het uitvoeren van eenvoudige transformaties, verkrijgen we de uitdrukking voor de macht P en de afhankelijkheid van de momentane waarde p (t) van de componenten van het product van de momentane stroom i (t) en spanning u (t).

Bepaling van constant elektrisch vermogen

V DC-circuits de grootte van de spanningsval in het circuitgedeelte en de stroom die er doorheen vloeit, verandert niet en blijft stabiel, gelijk aan de momentane waarden.Daarom kan het vermogen in dit circuit worden bepaald door deze waarden te vermenigvuldigen of het perfecte werk A te delen door de periode van uitvoering, zoals weergegeven in de verklarende afbeelding.

Bepaling van wisselstroom elektrisch vermogen

De wetten van sinusoïdale variatie van stromen en spanningen die door elektrische netwerken worden verzonden, leggen hun invloed op de uitdrukking van vermogen in dergelijke circuits. Hier komt het schijnbare vermogen om de hoek kijken, dat wordt beschreven door de vermogensdriehoek en bestaat uit actieve en reactieve componenten.

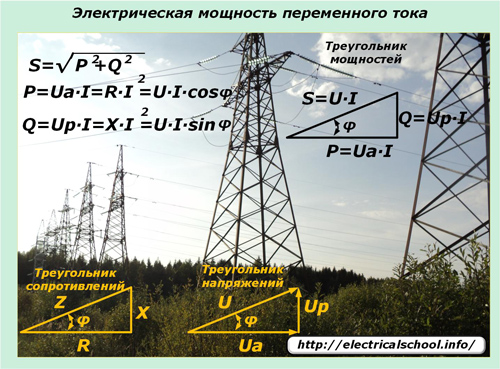
Een sinusvormige elektrische stroom bij het passeren van hoogspanningslijnen met gemengde soorten belastingen in alle secties verandert de vorm van de harmonische niet.En de spanningsval bij reactieve belastingen verschuift in fase in een bepaalde richting. Momentwaarde-uitdrukkingen helpen om het effect van toegepaste belastingen op de vermogensverandering in het circuit en zijn richting te begrijpen.

Let er tegelijkertijd onmiddellijk op dat de richting van de stroom van de generator naar de consument en het uitgezonden vermogen door het gecreëerde circuit totaal verschillende dingen zijn, die in sommige gevallen niet alleen niet samenvallen, maar ook zijn in tegengestelde richtingen gericht.

Beschouw deze relaties in hun ideale, pure manifestatie voor verschillende soorten belastingen:

• actief;

• capacitief;

• inductief.

Vermogensdissipatie actieve belasting

We gaan ervan uit dat de generator een ideale sinusvormige spanning u produceert die wordt toegepast op de zuiver actieve weerstand van het circuit. Ampèremeter A en voltmeter V meten stroom I en spanning U telkens t.

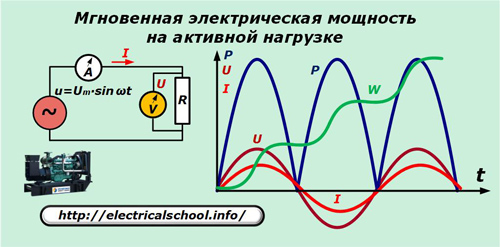
De grafiek laat zien dat de sinusoïden van de stroom en de spanningsval over de actieve weerstand overeenkomen in frequentie en fase, waardoor dezelfde oscillaties ontstaan. De kracht uitgedrukt door hun product oscilleert met tweemaal de frequentie en blijft altijd positief.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Als we naar de uitdrukking gaan werkspanning, dan krijgen we: p = P ∙ (1-cos2ωt).

We zullen dan het vermogen over de periode van één oscillatie T integreren en we zullen kunnen opmerken dat de energiewinst ∆W gedurende dit interval toeneemt. Na verloop van tijd blijft de weerstand nieuwe delen elektriciteit verbruiken, zoals te zien is in de grafiek.

Bij reactieve belastingen zijn de kenmerken van het energieverbruik anders, ze hebben een andere vorm.

Capacitieve vermogensdissipatie

Vervang in het elektrische circuit van de generator het weerstandselement door een condensator met capaciteit C.

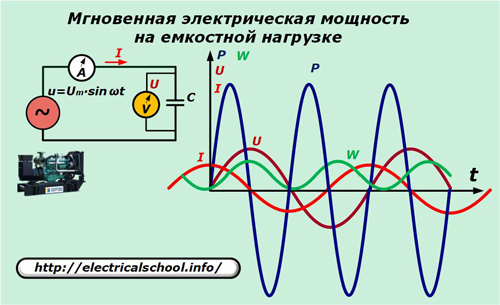
De relatie tussen de stroom en de spanningsval in de capaciteit wordt uitgedrukt door de verhouding: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

We vermenigvuldigen de waarden van de momentane uitdrukkingen van stroom met spanning en krijgen de waarde van het vermogen dat wordt verbruikt door de capacitieve belasting.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt.

Hier kun je zien dat het vermogen rond nul fluctueert bij tweemaal de frequentie van de aangelegde spanning. De totale waarde voor de harmonische periode, evenals de energiewinst, is nul.

Dit betekent dat energie langs het gesloten circuit van het circuit in beide richtingen beweegt, maar niet werkt.Een dergelijk feit wordt verklaard door het feit dat wanneer de bronspanning in absolute waarde toeneemt, het vermogen positief is en de energiestroom door het circuit naar de container wordt geleid, waar energie wordt geaccumuleerd.

Nadat de spanning is overgegaan naar de dalende harmonische sectie, wordt energie teruggevoerd van de condensator naar het circuit naar de bron. In geen van beide processen wordt nuttig werk verricht.

Vermogensdissipatie in een inductieve belasting

Vervang nu in het voedingscircuit de condensator door zelfinductie L.

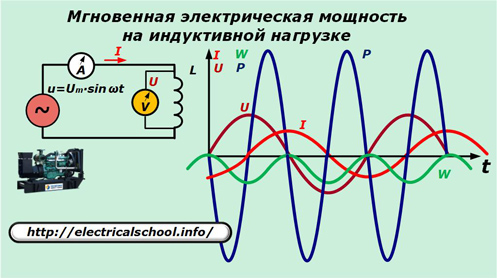
Hier wordt de stroom door de inductantie uitgedrukt door de verhouding:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Dan krijgen we

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ (2ХL) ∙ sin2ωt.

De resulterende uitdrukkingen stellen ons in staat om de aard van de verandering in de richting van de kracht en de toename van energie op de inductantie te zien, die dezelfde oscillaties uitvoeren die nutteloos zijn om werk te doen, als op de capaciteit.

Het vermogen dat vrijkomt bij reactieve belastingen wordt reactieve component genoemd. In ideale omstandigheden, wanneer de aansluitdraden geen actieve weerstand hebben, lijkt het onschadelijk en veroorzaakt het geen schade. Maar in echte stroomomstandigheden veroorzaken periodieke transiënten en schommelingen in blindvermogen opwarming van alle actieve elementen, inclusief verbindingsdraden, waarvoor wat energie wordt verbruikt en de waarde van het toegepaste volledige vermogen van de bron afneemt.

Het belangrijkste verschil tussen de reactieve component van vermogen is dat het helemaal geen nuttig werk verricht, maar leidt tot verlies van elektrische energie en overmatige belasting van apparatuur, wat vooral gevaarlijk is in kritieke situaties.

Om deze redenen, om de invloed van reactief vermogen te elimineren, in het bijzonder technische systemen voor zijn vergoeding.

Vermogensverdeling bij gemengde belasting

Als voorbeeld gebruiken we de belasting van een generator met een actieve capacitieve karakteristiek.

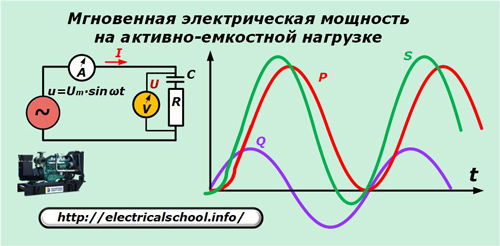
Om het beeld te vereenvoudigen, worden de sinusoïden van stromen en spanningen niet weergegeven in de gegeven grafiek, maar er moet rekening mee worden gehouden dat bij een actief-capacitieve aard van de belasting de stroomvector de spanning leidt.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Na transformaties krijgen we: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Deze twee termen in de laatste uitdrukking zijn de actieve en reactieve componenten van het momentane schijnbare vermogen. Alleen de eerste hiervan doet nuttig werk.

Hulpmiddelen voor het meten van vermogen

Om het elektriciteitsverbruik te analyseren en ervoor te berekenen, worden meetapparatuur gebruikt, die al lang wordt genoemd «Tellers»… Hun werk is gebaseerd op het meten van de effectieve waarden van stroom en spanning en deze automatisch vermenigvuldigen met een output van informatie.

Meters geven het energieverbruik weer door de bedrijfstijd van elektrische apparaten stapsgewijs te tellen vanaf het moment dat de meter onder belasting wordt ingeschakeld.

Om de actieve component van vermogen in AC-circuits te meten, wattmeters, en reactieve - varmeters. Ze hebben verschillende eenheidsaanduidingen:

• watt (W, W);

• var (var, var, var).

Om het totale energieverbruik te bepalen, is het noodzakelijk om de waarde ervan te berekenen met behulp van de vermogensdriehoekformule op basis van de waarden van de wattmeter en varmeter. Het wordt uitgedrukt in zijn eigen eenheden - volt-ampère.

De geaccepteerde benamingen van de eenheden van elk helpen elektriciens om niet alleen de waarde ervan te beoordelen, maar ook de aard van de vermogenscomponent.