RMS-waarden van stroom en spanning

De sinusvormige wisselstroom heeft gedurende de periode verschillende momentane waarden. Het is normaal om de vraag te stellen, welke stroomwaarde zal worden gemeten met de ampèremeter die in het circuit is opgenomen?

Bij het berekenen van wisselstroomcircuits, evenals elektrische metingen, is het onhandig om momentane of amplitudewaarden van stromen en spanningen te gebruiken, en hun gemiddelde waarden over een periode zijn nul. Bovendien kan het elektrische effect van een periodiek veranderende stroom (de hoeveelheid warmte die vrijkomt, de perfecte werking, enz.) niet worden ingeschat door de amplitude van deze stroom.

Het handigst was de introductie van de concepten van de zogenaamde effectieve waarden van stroom en spanning... Deze concepten zijn gebaseerd op de thermische (of mechanische) actie van de stroom, die niet afhankelijk is van de richting ervan.

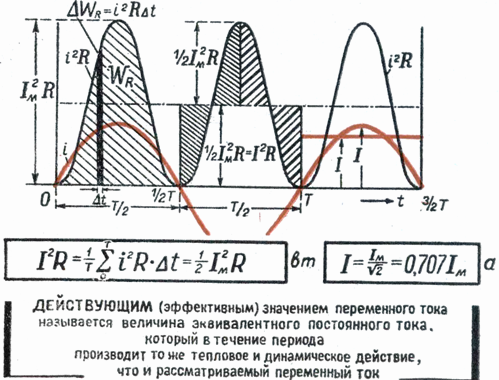
Wortelgemiddelde kwadratische waarde van wisselstroom - dit is de waarde van gelijkstroom waarbij tijdens de periode van wisselstroom dezelfde hoeveelheid warmte vrijkomt in de geleider als tijdens wisselstroom.

Om de ondernomen acties te evalueren wisselstroom, zullen we zijn acties vergelijken met het thermische effect van gelijkstroom.

Gelijkstroom P A die door weerstand r gaat, is P = P2r.

AC-vermogen wordt uitgedrukt als het gemiddelde effect van het momentane vermogen Az2r over de gehele periode of het gemiddelde van (I am x sinωT)2 NS r voor dezelfde tijd.

Laat de gemiddelde waarde van t2 voor de periode M zijn. Als we het vermogen van gelijkstroom en het vermogen van wisselstroom gelijkstellen, krijgen we: Az2r = Mr -n, vandaar Az = √M,

De grootheid I wordt de effectieve waarde van de wisselstroom genoemd.

De gemiddelde waarde van i2 bij wisselstroom wordt als volgt bepaald.

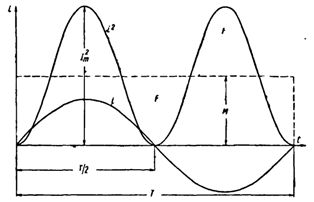
Laten we een sinusvormige stroomcurve construeren. Door elke momentane stroomwaarde te kwadrateren, verkrijgen we een P versus tijd-curve.

AC rms-waarde

Beide helften van deze curve liggen boven de horizontale as, aangezien de negatieve stromen (-i) in de tweede helft van de periode, gekwadrateerd, positieve waarden geven.

Construeer een rechthoek met basis T en een oppervlakte gelijk aan de oppervlakte begrensd door de kromme i2 en de horizontale as. De hoogte van de rechthoek M komt overeen met de gemiddelde waarde van P voor de periode. Deze periodewaarde, berekend met behulp van hogere wiskunde, zal gelijk zijn aan 1/2 I2m... Daarom is M. = 1/2 I2m

Aangezien de rms-waarde Im wisselstroom Im = √M is, dan is uiteindelijk I = Im / √2

Evenzo heeft de relatie tussen de rms- en amplitudewaarden voor de spanning U en E de vorm:

U = Um / √2E = Em / √2

De effectieve waarden van de variabelen worden aangegeven met hoofdletters zonder subscript (I, U, E).

Op basis van het bovenstaande kunnen we zeggen dat de effectieve waarde van een wisselstroom gelijk is aan zo'n gelijkstroom, die door dezelfde weerstand als de wisselstroom gaat en tegelijkertijd dezelfde hoeveelheid energie vrijgeeft.

Elektrische meetinstrumenten (ampèremeters, voltmeters) die in een wisselstroomcircuit zijn opgenomen, geven de effectieve waarden van stroom of spanning aan.

Bij het construeren van vectordiagrammen is het handiger om niet de amplitude, maar de effectieve waarden van de vectoren uit te stellen. Hiervoor worden de lengtes van de vectoren eenmaal met √2 verminderd. Dit verandert niets aan de locatie van de vectoren in het diagram.