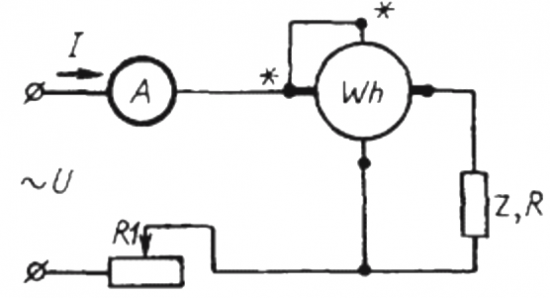
Het principe en de methoden van indirecte bepaling van de arbeidsfactor in het wisselstroomcircuit

Vermogensfactor of cosinus phi, t.o.v. de gebruiker van sinusvormige wisselstroom, is de verhouding van het actieve stroomverbruik P tot het totale vermogen S dat vanuit het netwerk aan deze gebruiker wordt geleverd.

Totaal vermogen S, in het algemeen, kan worden gedefinieerd als het product van de effectieve (root mean square) waarden van de stroom I en de spanning U in het beschouwde circuit, en het actieve vermogen P - zoals onomkeerbaar verbruikt door de gebruiker voor de werking van het werk.

Reactief vermogen Q, hoewel het deel uitmaakt van het totale vermogen, wordt het echter niet verbruikt om werk uit te voeren, maar neemt het alleen deel aan het creëren van wisselende elektrische en magnetische velden in sommige elementen van het circuit van de gebruiker.

behalve directe meting van de arbeidsfactor gebruik van elektrodynamische apparaten - fase meter, zijn er vrij logische indirecte methoden waarmee u wiskundig nauwkeurig de waarde kunt begrijpen van deze zeer belangrijke elektrische grootheid die de gebruiker kenmerkt in een sinusoïdaal wisselstroomcircuit.

Laten we naar de gegevens kijken indirecte methoden in detail, Laten we het principe van indirecte arbeidsfactormeting begrijpen.

Voltmeter, ampèremeter en wattmeter methode

Elektrodynamische wattmeter met extra actieve weerstand in het circuit van zijn bewegende spoel geeft de waarde aan van extreem actief vermogen dat wordt verbruikt in het AC-circuit P.

Als we nu met behulp van een voltmeter en een ampèremeter de gemiddelde waarden meten van de stroom I en de spanning U die in het circuit van de bestudeerde belasting werken, dan krijgen we door deze twee parameters te vermenigvuldigen alleen het totale vermogen S .

Dan kan de arbeidsfactor (cosinus phi) van een bepaalde belasting eenvoudig worden gevonden met behulp van de formule:

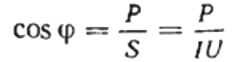
Hier kunt u desgewenst ook de waarde vinden van het blindvermogen Q, de totale weerstand van de schakeling z De wet van Ohm, evenals actieve en reactieve weerstand, simpelweg door een weerstandsdriehoek te construeren of weer te geven en vervolgens de stelling van Pythagoras te gebruiken:

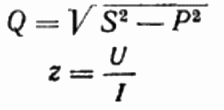
Teller- en ampèremetermethode

Om deze methode te gebruiken, is het noodzakelijk om een ​​circuit samen te stellen waarin de eenvoudigste in serie is geschakeld met de belasting Z en de ampèremeter elektriciteitsmeter Wh.

Gedurende een bepaalde tijd t, in de orde van een minuut, zal het nodig zijn om het aantal omwentelingen van de schijf N te berekenen, wat de hoeveelheid actieve energie zal weergeven die gedurende een bepaalde tijd is verbruikt (dwz rekening houdend met de krachtfactor).

Hier: het aantal omwentelingen van de schijf N, de coëfficiënt k is de hoeveelheid energie per omwenteling, I en U zijn respectievelijk de rms stroom en spanning, t is de tijd voor het tellen van de omwentelingen, cosinus phi is de arbeidsfactor:

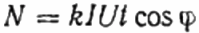
Vervolgens wordt, in plaats van de bestudeerde gebruiker Z, de actieve belasting R in het circuit opgenomen via dezelfde teller, maar niet rechtstreeks, maar via de reostaat R1 (het bereiken van dezelfde stroom I als in het eerste geval, met de gebruiker Z). Het aantal omwentelingen van de schijf N1 wordt gedurende dezelfde tijd t behouden. Maar hier, aangezien de belasting actief is, is de cosinus phi (power factor) zeker gelijk aan 1. Vandaar:

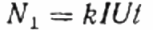
Vervolgens wordt de verhouding van de omwentelingen van de schijfteller geregistreerd voor dezelfde periode in het eerste en tweede geval.Dit is cosinus phi, dat wil zeggen de arbeidsfactor van de eerste belasting (ten opzichte van een puur actieve belasting met dezelfde huidig):

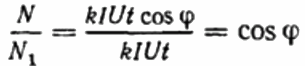
Drie ampèremeter methode

Om de vermogensfactor in een sinusvormige stroomkring met behulp van drie ampèremeters te bepalen, moet u eerst de volgende schakeling samenstellen:

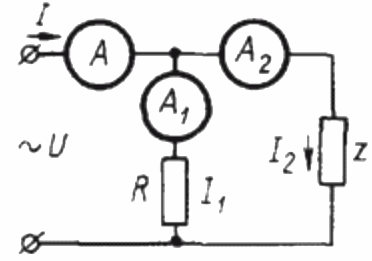
Hier is Z een belasting waarvan de vermogensfactor moet worden bepaald en R is een puur actieve belasting.

Aangezien de belasting R puur actief is, is de stroom I1 op elk moment in fase met de wisselspanning U die op deze belasting wordt toegepast.In dit geval is de stroom I gelijk aan de geometrische som van de stromen I1 en I2. Nu bouwen we op basis van deze positie een vectordiagram van de stromingen:

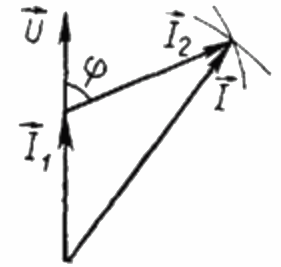
Op het vectordiagram van de stromen is de scherpe hoek tussen de stroom I1 en de stroom I2 de hoek phi, waarvan de cosinus (in feite de waarde van de arbeidsfactor) kan worden gevonden in een speciale tabel met waarden van goniometrische functies of berekend met de formule:

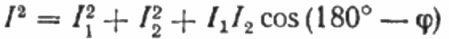
Vanaf hier kunnen we cosinus phi uitdrukken, dat wil zeggen de gewenste arbeidsfactor:

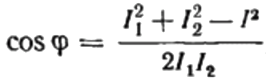
Het teken van de gevonden vermogensfactor («+» of «-«) geeft de aard van de belasting aan. Als de vermogensfactor (cosinus phi) negatief is, is de belasting capacitief van aard. Als de vermogensfactor een positieve waarde is, is de aard van de belasting inductief.