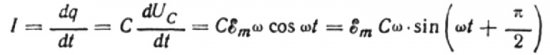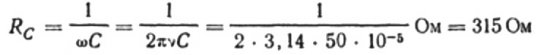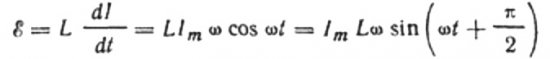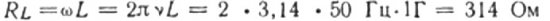Capacitieve en inductieve weerstand in een wisselstroomcircuit

Als we een condensator in een gelijkstroomcircuit opnemen, ontdekken we dat deze een oneindige weerstand heeft omdat een gelijkstroom eenvoudigweg niet door het diëlektricum tussen de platen kan gaan, aangezien een diëlektricum per definitie geen gelijkstroom geleidt.

Een condensator verbreekt het gelijkstroomcircuit. Maar als dezelfde condensator nu is opgenomen in het wisselstroomcircuit, dan blijkt dat de condensator niet volledig lijkt te breken, hij wisselt gewoon af en laadt op, dat wil zeggen, de elektrische lading beweegt en de stroom in het externe circuit is onderhouden.

Op basis van de theorie van Maxwell kunnen we in dit geval zeggen dat de wisselende geleidingsstroom in de condensator nog steeds gesloten is, alleen in dit geval - door de biasstroom. Dit betekent dat de condensator in het AC-circuit fungeert als een soort eindige weerstand. Deze weerstand wordt genoemd capacitief.

De praktijk leert al lang dat de hoeveelheid wisselstroom die door een geleider vloeit afhangt van de vorm van die geleider en van de magnetische eigenschappen van het medium eromheen.Bij een rechte draad zal de stroom het grootst zijn, en als dezelfde draad met een groot aantal windingen in een spoel wordt gewikkeld, zal de stroom minder zijn.

En als een ferromagnetische kern in dezelfde spoel wordt ingebracht, zal de stroom nog meer afnemen. De draad levert dus niet alleen wisselstroom met een ohmse (actieve) weerstand, maar ook met een extra weerstand, afhankelijk van de inductantie van de draad. Deze weerstand wordt genoemd inductief.

De fysieke betekenis ervan is dat een veranderende stroom in een geleider met een bepaalde inductantie een EMF van zelfinductie in die geleider initieert, die de neiging heeft om veranderingen in de stroom te voorkomen, dat wil zeggen, de neiging heeft om de stroom te verminderen. Dit komt overeen met het verhogen van de weerstand van de draad.

Capaciteit in het wisselstroomcircuit

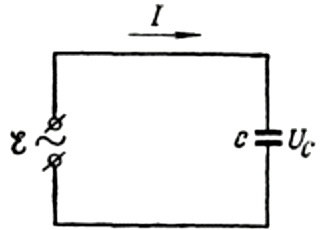
Laten we eerst de capacitieve weerstand in meer detail bespreken. Stel dat een condensator met capaciteit C is aangesloten op een sinusvormige wisselstroombron, dan wordt de EMF van deze bron beschreven met de volgende formule:

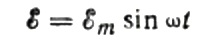
We zullen de spanningsval over de aansluitdraden negeren, omdat deze meestal erg klein is en indien nodig afzonderlijk kan worden beschouwd. Laten we nu aannemen dat de spanning over de condensatorplaten gelijk is aan de AC-bronspanning. Dan:

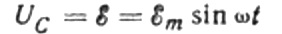
Op elk moment hangt de lading op een condensator af van zijn capaciteit en de spanning tussen zijn platen. Dan, gegeven de bekende bron die hierboven werd genoemd, krijgen we een uitdrukking voor het vinden van de lading op de condensatorplaten door de bronspanning:

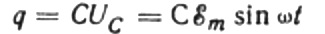
Laat gedurende een oneindig kleine tijd dt de lading op de condensator veranderen met dq, dan zal er een stroom I door de draden van de bron naar de condensator vloeien gelijk aan:

De waarde van de huidige amplitude is gelijk aan:

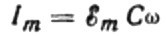
Dan is de uiteindelijke uitdrukking voor de stroom:

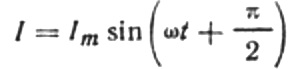
Laten we de formule voor de huidige amplitude als volgt herschrijven:

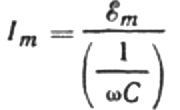
Deze verhouding is de wet van Ohm, waar het omgekeerde van het product van hoekfrequentie en capaciteit de rol van weerstand speelt, en is eigenlijk een uitdrukking voor het vinden van de capaciteit van een condensator in een sinusvormige wisselstroomschakeling:

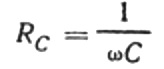
Dit betekent dat de capacitieve weerstand omgekeerd evenredig is met de hoekfrequentie van de stroom en de capaciteit van de condensator. Het is gemakkelijk om de fysieke betekenis van deze afhankelijkheid te begrijpen.

Hoe groter de capaciteit van de condensator in het AC-circuit en hoe vaker de richting van de stroom in dat circuit verandert, hoe meer totale lading er per tijdseenheid door de dwarsdoorsnede van de draden gaat die de condensator met de AC-bron verbinden. Dit betekent dat de stroom evenredig is met het product van de capaciteit en de hoekfrequentie.

Laten we bijvoorbeeld de capaciteit berekenen van een condensator met een elektrische capaciteit van 10 microfarad voor een sinusvormig wisselstroomcircuit met een frequentie van 50 Hz:

Als de frequentie 5000 Hz was, zou dezelfde condensator een weerstand van ongeveer 3 ohm hebben.

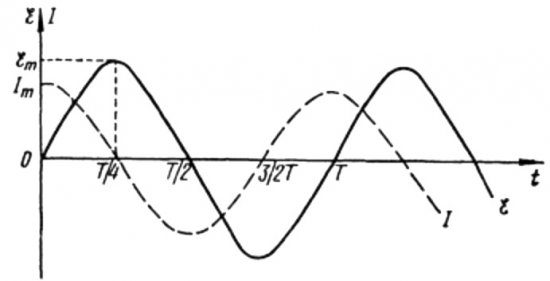
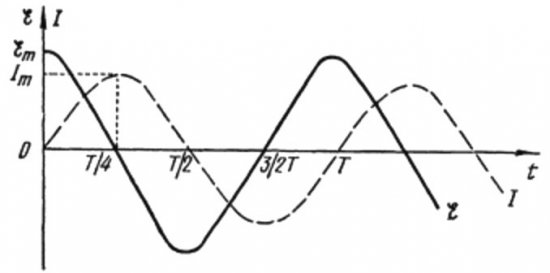
Uit bovenstaande formules is duidelijk dat de stroom en spanning in een wisselstroomcircuit met een condensator altijd in verschillende fasen veranderen. De stroomfase loopt pi/2 (90 graden) voor op de spanningsfase. Dit betekent dat de maximale stroom in de tijd altijd een kwart periode eerder is dan de maximale spanning. Dus over de capacitieve weerstand loopt de stroom een ​​kwart van de tijdsperiode voor op de spanning, of 90 graden in fase.

Laten we de fysieke betekenis van dit fenomeen uitleggen.Op het eerste moment is de condensator volledig ontladen, dus de geringste spanning die erop wordt toegepast, verplaatst de ladingen op de platen van de condensator al, waardoor er een stroom ontstaat.

Naarmate de condensator oplaadt, neemt de spanning over de platen toe, dit voorkomt verdere stroom van lading, dus de stroom in het circuit neemt af ondanks verdere toename van de spanning die op de platen wordt toegepast.

Dit betekent dat als op het beginmoment de stroom maximaal was, de stroom volledig stopt wanneer de spanning na een kwart periode zijn maximum bereikt.

Aan het begin van de periode is de stroom maximaal en de spanning minimaal en begint te stijgen, maar na een kwart van de periode bereikt de spanning een maximum, maar de stroom is tegen die tijd al tot nul gedaald. Zo blijkt dat de spanning een kwart van de periode voorloopt op de spanning.

AC inductieve weerstand

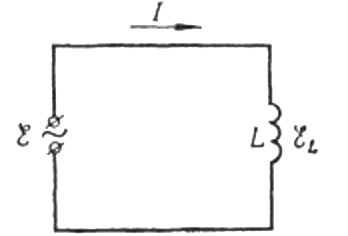
Nu terug naar inductieve weerstand. Neem aan dat een wisselende sinusvormige stroom door een inductantiespoel vloeit. Het kan worden uitgedrukt als:

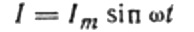
De stroom is het gevolg van de wisselspanning die op de spoel wordt toegepast. Dit betekent dat er een EMF van zelfinductie op de spoel verschijnt, die als volgt wordt uitgedrukt:

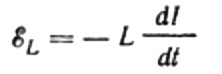
Nogmaals, we verwaarlozen de spanningsval over de draden die de EMF-bron verbinden met de spoel. Hun ohmse weerstand is erg laag.

Laat de wisselspanning die op elk moment op de spoel wordt toegepast volledig in evenwicht worden gebracht door de opkomende EMF van zelfinductie die qua grootte gelijk is maar tegengesteld in richting:

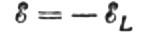
Dan hebben we het recht om te schrijven:

Aangezien de amplitude van de spanning die op de spoel wordt toegepast, is:

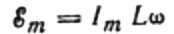
we krijgen:

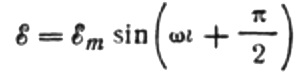
Laten we de maximale stroom als volgt uitdrukken:

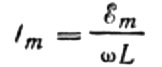
Deze uitdrukking is in wezen de wet van Ohm. Een grootheid gelijk aan het product van de inductantie en de hoekfrequentie speelt hier de rol van weerstand en is niets anders dan de inductieve weerstand van de inductor:

De inductieve weerstand is dus evenredig met de inductantie van de spoel en de hoekfrequentie van de wisselstroom door die spoel.

Dit komt door het feit dat inductieve weerstand het gevolg is van de invloed van zelfinductie EMF op de bronspanning, - zelfinductie EMF heeft de neiging de stroom te verminderen en brengt daarom weerstand in het circuit. De grootte van de emf van zelfinductie is, zoals bekend, evenredig met de inductantie van de spoel en de veranderingssnelheid van de stroom er doorheen.

Laten we bijvoorbeeld de inductieve weerstand berekenen van een spoel met een inductantie van 1 H, die is opgenomen in een circuit met een stroomfrequentie van 50 Hz:

Als de frequentie van de bal 5000 Hz was, dan zou de weerstand van dezelfde spoel ongeveer 31.400 ohm zijn.Bedenk dat de ohmse weerstand van de spoeldraad meestal een paar ohm is.

Uit de bovenstaande formules is het duidelijk dat de veranderingen in de stroom door de spoel en de spanning daarin in verschillende fasen optreden, en de fase van de stroom is altijd kleiner dan de fase van de spanning bij pi / 2. Daarom is de maximale stroom treedt een kwart periode later op dan het begin van maximale spanning.

Bij inductieve weerstand loopt de stroom 90 graden achter op de spanning vanwege het remmende effect van de zelfgeïnduceerde EMF, die voorkomt dat de stroom verandert (zowel toenemend als afnemend), dus de maximale stroom wordt later waargenomen in het circuit met de spoel dan de maximale spanning.

Spoel en condensator gecombineerde actie

Als je een spoel met een condensator in serie verbindt met een wisselstroomcircuit, dan zal de spoelspanning de condensatorspanning in de tijd een halve periode vooruitschuiven, dat wil zeggen 180 graden in fase.

Capacitieve en inductieve weerstand worden genoemd reactanten… Energie wordt niet verbruikt in reactieve weerstand zoals in actieve weerstand. De in de condensator opgeslagen energie wordt periodiek teruggevoerd naar de bron wanneer het elektrische veld in de condensator verdwijnt.

Het is hetzelfde met een spoel: aangezien het magnetische veld van de spoel wordt gecreëerd door de stroom, hoopt de energie erin zich op gedurende een kwart van de periode, en tijdens het volgende kwart van de periode keert het terug naar de bron. In dit artikel hebben we het gehad over sinusvormige wisselstroom, waarvoor deze voorschriften strikt worden gevolgd.

In AC-sinusoïdale circuits worden inductoren met kern genoemd verstikkendworden traditioneel gebruikt voor stroombegrenzing. Hun voordeel ten opzichte van reostaten is dat energie niet in grote hoeveelheden als warmte wordt gedissipeerd.