Definitie en uitleg van de regel van Lenz

Met de regel van Lenz kunt u de richting van de inductiestroom in het circuit bepalen. Hij zegt: «de richting van de inductiestroom is altijd zodanig dat de werking ervan het effect verzwakt van de oorzaak die deze inductiestroom veroorzaakt».

Als de baan van een bewegend geladen deeltje op enigerlei wijze verandert als gevolg van de interactie van het deeltje met een magnetisch veld, dan leiden deze veranderingen tot het verschijnen van een nieuw magnetisch veld, precies tegenovergesteld aan het magnetische veld dat deze veranderingen veroorzaakte.

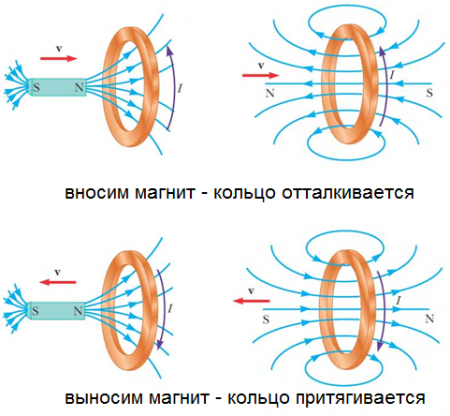
Als je bijvoorbeeld een kleine koperen ring neemt die aan een draad hangt en er met de noordpool sterk genoeg in probeert te rijden magneet, zodra de magneet de ring nadert, begint de ring de magneet af te stoten.

Het lijkt erop dat de ring zich begint te gedragen als een magneet, gericht naar dezelfde naam (in dit voorbeeld de noordpool) naar de magneet die erin is gestoken, en probeert zo de zogenaamde magneet te verzwakken.

En als je de magneet in de ring stopt en vanaf de ring begint te duwen, dan zal de ring integendeel de magneet volgen, alsof hij zich manifesteert als dezelfde magneet, maar nu - kijkend naar de tegenovergestelde pool van de trekkracht - uitgangsmagneet (we verplaatsen de noordpool van de magneet - de zuidpool gevormd op de ring wordt aangetrokken), dit keer proberen we het magnetische veld te versterken dat verzwakt is door de uitzetting van de magneet.

Als je hetzelfde doet met een open ring, dan zal de ring niet reageren op de magneet, hoewel er een EMF in wordt geïnduceerd, maar aangezien de ring niet gesloten is, zal er geen geïnduceerde stroom zijn en daarom hoeft zijn richting niet nader te bepalen.

Wat is hier echt aan de hand? Door een magneet in een complete ring te duwen, vergroten we de magnetische flux die de gesloten lus binnendringt, en daarom (van volgens de wet van Faraday van elektromagnetische inductieEMF gegenereerd in de ring is evenredig met de veranderingssnelheid van de magnetische flux) EMF wordt gegenereerd in de ring.

En door de magneet uit de ring te duwen, veranderen we ook de magnetische flux door de ring, alleen verhogen we deze nu niet, maar verkleinen we, en de resulterende EMF zal weer evenredig zijn met de veranderingssnelheid van de magnetische flux, maar in de tegenovergestelde richting gericht. Aangezien het circuit een gesloten ring is, genereert de EMF natuurlijk een gesloten stroom in de ring. En stroom creëert een magnetisch veld om zich heen.

De richting van de inductielijnen van het magnetische veld dat in de huidige ring wordt gegenereerd, kan worden bepaald door de gimlet-regel, en ze zullen precies zo worden gericht dat het gedrag van de inductielijnen van de geïntroduceerde magneet wordt voorkomen: de lijnen van een externe bron komt de ring binnen, en vanaf de ring gaan respectievelijk de lijnen van een externe bron de ring in, respectievelijk gaan ze.

Regel van Lenz in een transformator

Laten we ons nu herinneren hoe het, in overeenstemming met de regel van Lenz, is geladen net transformator… Stel dat de stroom toeneemt in de primaire wikkeling van de transformator, daarom neemt het magnetische veld in de kern toe. De magnetische flux die de secundaire wikkeling van de transformator binnendringt, neemt toe.

Omdat de secundaire wikkeling van de transformator wordt gesloten door de belasting, zal de daarin gegenereerde EMF een geïnduceerde stroom genereren, die zijn eigen magnetische veld op de secundaire wikkeling zal creëren. De richting van dit magnetische veld zal zodanig zijn dat het het magnetische veld van de primaire wikkeling verzwakt.Dit betekent dat de stroom in de primaire wikkeling zal toenemen (aangezien een toename van de belasting in de secundaire wikkeling gelijk staat aan een afname van de inductantie van de primaire wikkeling van de transformator, waardoor de impedantie van de nettransformator wordt verminderd). En het netwerk begint te werken in de primaire wikkeling van de transformator, waarvan de waarde afhangt van de belasting in de secundaire wikkeling.