Elektrische circuits met niet-sinusvormige stroom

Niet-sinusvormige stromen en hun ontbinding

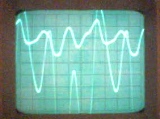In een elektrisch circuit kunnen om twee redenen niet-sinusvormige stromen optreden:

1. het elektrische circuit zelf is lineair, maar een niet-sinusvormige spanning werkt op het circuit,

2. de spanning die op het circuit werkt, is sinusvormig, maar het elektrische circuit bevat niet-lineaire elementen.

Er kunnen beide redenen zijn. Dit hoofdstuk behandelt alleen circuits voor het eerste punt. In dit geval worden de niet-sinusvormige spanningen als periodiek beschouwd.

Generatoren van periodieke pulsen worden gebruikt in verschillende apparaten van radiotechniek, automatisering, telemechanica. De vorm van de pulsen kan verschillen: zaag, getrapt, rechthoekig (fig. 1).

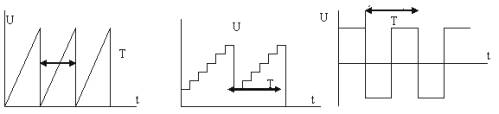
Figuur 1. Pulsvormen

De verschijnselen die optreden in een lineair elektrisch circuit onder periodieke maar niet-sinusvormige spanningen zijn het gemakkelijkst te bestuderen als de spanningscurve wordt uitgebreid in een trigonometrische Fourier-reeks:

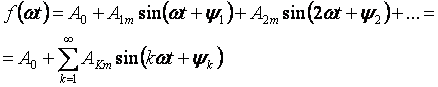
De eerste term van de reeks A0 wordt de constante component of nulde harmonische genoemd, de tweede term van de reeks

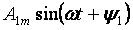
— de grondtoon of eerste harmonische en alle andere leden van de vorm

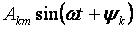
voor k > 1 worden hogere harmonischen genoemd.

Als we in uitdrukking (3.1) de sinus van de som openen, kunnen we naar een andere vorm van schrijven van de reeks gaan:

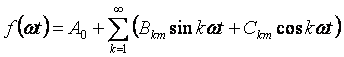Als de functie symmetrisch is om de abscis-as, bevat de reeks geen constante component. Als de functie symmetrisch is om de ordinatas, bevat de reeks geen sinussen. De functie is symmetrisch rond de oorsprong en bevat geen cosinussen.

Enkele voorbeelden van serie-uitbreiding worden in een tabel gegeven. 1 en ze zijn ook beschikbaar in de referentieliteratuur.

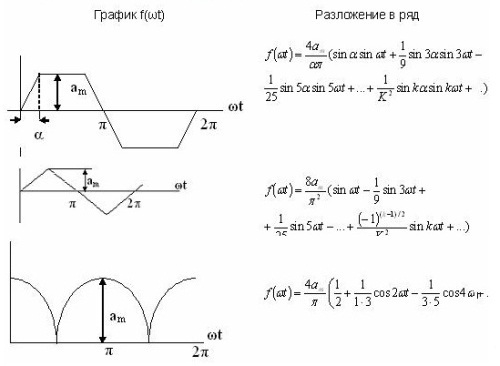
Tabel 1. Uitbreiding van de Fourier-reeks

Berekening van niet-sinusvormige stroomcircuits

Het circuit wordt berekend voor elke harmonische volgens het model. Het circuit wordt zo vaak berekend als er harmonischen zijn in de spanning die op het circuit werkt. In dit geval is het noodzakelijk om rekening te houden met een aantal kenmerken.

Opgemerkt moet worden dat de weerstand van het inductieve element toeneemt naarmate het harmonische getal toeneemt

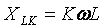
en het capacitieve element daarentegen neemt af:

Er moet ook rekening mee worden gehouden dat de constante component van de stroom niet door de condensator gaat en dat de inductantie er geen weerstand tegen is.

Bovendien mag men de mogelijke resonantieverschijnselen niet alleen bij de grondharmonische, maar ook bij hogere harmonischen niet vergeten.

Vectordiagrammen kan voor elke harmonische afzonderlijk worden geplot.

Volgens het principe van superpositie kan de stroom van elke tak bestaan ​​uit de som van individuele termen (nul, fundamentele en hogere harmonischen):

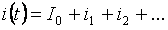
De effectieve waarde van de totale takstroom kan worden bepaald door de gemiddelde waarde van de individuele harmonische stromen:

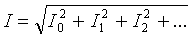
Het actief vermogen van de niet-sinusvormige stroom is gelijk aan de som van het actief vermogen van de individuele harmonischen:

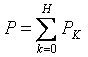
Hieronder vindt u een algemeen voorbeeld voor het berekenen van niet-sinusvormige stroomcircuits. Alle stromen, spanningen en weerstanden hebben twee indices: het eerste cijfer betekent het taknummer en het tweede cijfer het harmonische nummer. Ingangsspanning:

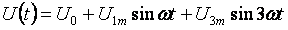
• Vast onderdeel

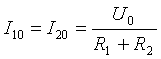
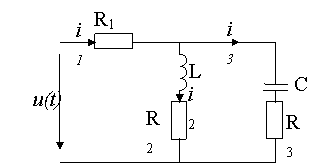
Figuur 2. Elektrisch schema

• Grote Harmonische:

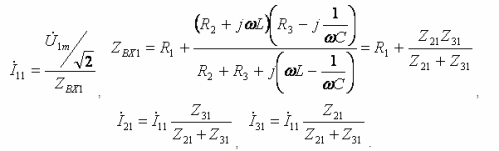
• Derde harmonische:

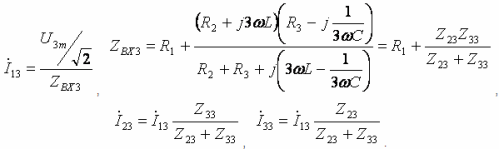
Lees ook: De meest voorkomende AC naar DC rectificatieschema's