Verliezen in AC-draden

Wanneer een wisselstroom door een geleider vloeit, wordt er om en in de geleider een wisselende magnetische flux gevormd, die b.v. D. s, die de inductieve weerstand van de draad bepaalt.

Als we de sectie van het stroomvoerende deel verdelen in verschillende elementaire geleiders, dan zullen degenen die zich in het midden van de sectie en er dichtbij bevinden de grootste inductieve weerstand hebben, omdat ze worden bedekt door de volledige magnetische flux - extern en intern. Elementaire geleiders die zich aan het oppervlak bevinden, worden alleen bedekt door de externe magnetische flux en hebben daarom de laagste inductieve weerstand.

Daarom neemt de elementaire inductieve weerstand van de geleiders toe vanaf het oppervlak naar het midden van de geleider.

Door de werking van afwisselende magnetische flux, oppervlakte-effect of huideffect, is er een verplaatsing van flux en stroom van de as van de geleider naar het oppervlak ervan, in de buitenste olifant; de stromen van de afzonderlijke lagen verschillen in grootte en fase.

Op een afstand Z0 van het oppervlak nemen de amplitude van de elektrische en magnetische velden en de stroomdichtheid af met e = 2,718 keer en bereiken ze 36% van hun oorspronkelijke waarde aan het oppervlak. Deze afstand wordt de penetratiediepte van het huidige veld genoemd en is gelijk aan

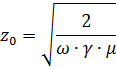
waarbij ω de hoekfrequentie van de wisselstroom is; γ — specifieke geleidbaarheid, 1 / ohm • cm, voor koper γ = 57 • 104 1 / ohm • cm; µ = µ0 • µr µ0 = 4 • π • 10-9 gn / cm — magnetische constante; µr is de relatieve magnetische permeabiliteit, gelijk aan 1 voor koper en aluminium.

In de praktijk wordt aangenomen dat het grootste deel van de stroom in de oppervlaktelaag van de geleider gaat met een dikte gelijk aan de penetratiediepte Z0, en het resterende deel, intern, deel van de doorsnede praktisch geen stroom geleidt en is niet gebruikt voor energieoverdracht.

In afb. 1 toont de stroomdichtheidsverdeling in een cirkelvormige geleider bij verschillende verhoudingen van geleiderradius tot penetratiediepte.

Het veld verdwijnt volledig op een afstand van het oppervlak gelijk aan 4 — 6 Z0.

Hieronder volgen de waarden van de indringdiepte Z0 in mm voor sommige geleiders bij een frequentie van 50 Hz:

Koper — 9,44, aluminium — 12,3, staal (µr = 200) — 1,8

De ongelijke verdeling van de stroom langs de dwarsdoorsnede van de geleider leidt tot een aanzienlijke verkleining van de dwarsdoorsnede van het eigenlijke stroomvoerende deel en dus tot een toename van de actieve weerstand.

Naarmate de actieve weerstand van de geleider Ra toeneemt, nemen de warmteverliezen daarin toe I2Ra, en daarom zullen bij dezelfde waarde van de stroom de verliezen in de geleider en de temperatuur van zijn verwarming met wisselstroom altijd groter zijn dan met gelijkstroom huidig.

Een maat voor het oppervlakte-effect is de oppervlakte-effectcoëfficiënt kp, die de verhouding weergeeft van de actieve weerstand van de geleider Ra tot zijn ohmse weerstand R0 (bij gelijkstroom).

De actieve weerstand van de geleider is

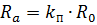
Het fenomeen van het oppervlakte-effect is sterker naarmate de doorsnede van de draad groter is magnetische permeabiliteit en hoger wisselstroom frequentie.

In massieve niet-magnetische geleiders, zelfs bij voedingsfrequentie, is het oppervlakte-effect zeer uitgesproken. Zo is de weerstand van een ronde koperdraad met een diameter van 24 cm bij 50 Hz wisselstroom ongeveer 8 keer hoger dan de weerstand bij gelijkstroom.

De skin-effectcoëfficiënt zal kleiner zijn, hoe groter de ohmse weerstand van de geleider; kn voor koperdraden zal bijvoorbeeld groter zijn dan voor aluminium met dezelfde diameter (doorsnede), omdat de weerstand van aluminium 70% hoger is dan die van koper. Aangezien de weerstand van de geleider toeneemt bij verhitting, zal de penetratiediepte toenemen bij toenemende temperatuur en kn zal afnemen.

In draden gemaakt van magnetische materialen (staal, gietijzer, etc.), ondanks hun hoge weerstand, manifesteert het oppervlakte-effect zich met extreme sterkte vanwege hun hoge magnetische permeabiliteit.

De oppervlakte-effectcoëfficiënt voor dergelijke draden, zelfs met kleine doorsneden, is 8-9. Bovendien hangt de waarde ervan af van de waarde van de stroom die vloeit. De aard van de weerstandsverandering komt overeen met de magnetische permeabiliteitscurve.

Een soortgelijk fenomeen van stroomherverdeling langs de doorsnede treedt op vanwege het nabijheidseffect, dat wordt veroorzaakt door het sterke magnetische veld van aangrenzende draden. De invloed van het nabijheidseffect kan in aanmerking worden genomen met behulp van de nabijheidscoëfficiënt kb, beide fenomenen — de coëfficiënt van extra verliezen:

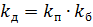
Voor hoogspanningsinstallaties met een voldoende grote afstand tussen de fasen wordt de coëfficiënt van bijkomende verliezen voornamelijk bepaald door het oppervlakte-effect, aangezien in dit geval het nabijheidseffect erg zwak is. Daarom beschouwen we in het volgende alleen de invloed van het oppervlakte-effect op stroomvoerende geleiders.

Rijst. 1 laat zien dat voor grote doorsneden alleen buisvormige of holle geleiders moeten worden gebruikt, aangezien bij een massieve geleider het middelste deel niet volledig wordt gebruikt voor elektrische doeleinden.

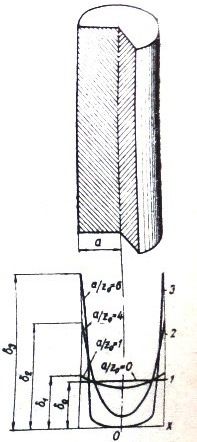
Rijst. 1. Verdeling van de stroomdichtheid in een ronde geleider bij verschillende verhoudingen α / Z0

Deze conclusies worden gebruikt bij het ontwerp van stroomvoerende delen van hoogspanningsschakelaars, scheiders, bij het ontwerp van rails en rails van hoogspanningsschakelaars.

Bepaling van de actieve weerstand Ra is een van de belangrijke problemen bij de praktische berekening van stroomvoerende delen en rails met verschillende profielen.

De actieve weerstand van de geleider wordt empirisch bepaald op basis van de gemeten totale vermogensverliezen erin, als een verhouding van de totale verliezen tot het kwadraat van de stroom:

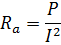
Het is moeilijk om de actieve weerstand van een geleider analytisch te bepalen, daarom worden voor praktische berekeningen berekende curven gebruikt, analytisch geconstrueerd en experimenteel geverifieerd.Meestal kunt u hiermee de huideffectfactor vinden als een functie van een ontwerpparameter die wordt berekend op basis van de geleiderkarakteristieken.

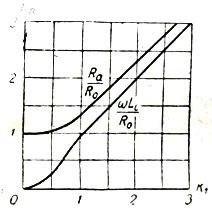
In afb. 2 toont krommen voor het bepalen van het oppervlakte-effect van niet-magnetische geleiders. De oppervlakte-effectcoëfficiënt van deze krommen wordt gedefinieerd als kn = f (k1), een functie van de berekende parameter k1, die is

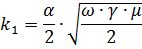
waar α de straal van de draad is, zie

Rijst. 2. Actieve en inductieve weerstand van de geleider bij wisselstroom

Bij een industriële frequentie van 50 Hz is het mogelijk om het oppervlakte-effect te negeren voor koperen geleiders d <22 mm en voor aluminium geleiders d <30 mm, aangezien voor hen kp <1,04

Verlies van elektrische energie kan worden uitgevoerd in niet-stroomvoerende delen die in een extern wisselend magnetisch veld vallen.

Gewoonlijk moeten wisselstroomgeleiders in elektrische machines, apparaten en schakelapparatuur zich dicht bij bepaalde delen van de constructie van magnetische materialen (staal, gietijzer, enz.) bevinden. Dergelijke onderdelen zijn onder meer metalen flenzen van elektrische apparatuur en ondersteunende constructies van rails, verdeelinrichtingen, versterking van onderdelen van gewapend beton in de buurt van bussen.

Onder invloed van een wisselende magnetische flux ontstaan ​​er een aantal stromende stromen in die delen die geen stroom voeren wervelstromen en hun magnetisatie-omkering vindt plaats. Zo ontstaan ​​energieverliezen in de omliggende staalconstructies door wervelstromen en door hysteresevolledig omgezet in warmte.

De wisselende magnetische flux in magnetische materialen dringt door tot een kleine diepte Z0, gemeten, zoals bekend, enkele millimeters.Wervelverliezen zullen daarbij ook geconcentreerd zijn in de dunne buitenlaag Z0.In dezelfde laag zullen ook hysteresisverliezen optreden.

Deze en andere verliezen kunnen afzonderlijk of samen worden verantwoord met behulp van verschillende, meestal semi-empirische formules.