De wet van Ohm voor een magnetisch circuit

Als er geen magnetische fluxen zouden zijn, is het onwaarschijnlijk dat moderne elektrotechniek zou bestaan. De werking van generatoren en elektromotoren, elektromagneten en transformatoren, meetinstrumenten en Hall-sensoren is gebaseerd op het gebruik van het magnetische veld en de eigenschappen van de magnetische flux.

Om de magnetische flux te concentreren en te versterken, nemen ze hun toevlucht tot het gebruik van ferromagnetische materialen. Ferromagnetische materialen worden geproduceerd magnetische kernen — lichamen van de vereiste vormen en afmetingen, kernen voor het richten van magnetische fluxen van een of andere grootte in de gewenste richting. Dergelijke lichamen, waarbinnen gesloten lijnen van magnetische inductie passeren, worden magnetische circuits genoemd.

De bekende eigenschappen van het magnetische veld maken het mogelijk om de magnetische fluxen in verschillende magnetische circuits te berekenen. Maar voor praktisch werk is het veel handiger om toevlucht te nemen tot algemene consequenties en wetten van magnetische circuits die zijn afgeleid van de wetten van het magnetische veld, in plaats van deze wetten elke keer rechtstreeks te gebruiken. Het toepassen van bepaalde regels op magnetische circuits is handiger voor het oplossen van typische praktische problemen.

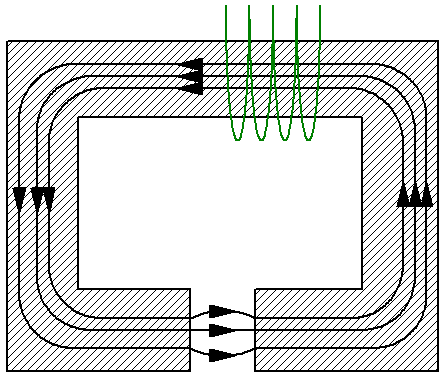
Beschouw bijvoorbeeld een eenvoudig magnetisch circuit dat bestaat uit een onvertakt juk met doorsnede S, dat op zijn beurt is gemaakt van een materiaal met doorlaatbaarheid mu… Het juk heeft een niet-magnetische spleet van hetzelfde gebied S, bijvoorbeeld lucht, en de magnetische permeabiliteit in de spleet - mu1 - verschilt van de magnetische permeabiliteit van het juk. Hier kun je naar de gemiddelde inductielijn kijken en de magnetische spanningsstelling erop toepassen:

Aangezien de lijnen van magnetische inductie continu zijn door het hele circuit, is de grootte van de magnetische flux in zowel het juk als de opening hetzelfde. Nu gebruiken we de formules voor magnetische inductie B en voor de magnetische flux F om de sterkte H van het magnetische veld uit te drukken in termen van de magnetische flux F.

De volgende stap is om de resulterende uitdrukkingen te vervangen door de bovenstaande formule van de magnetische fluxstelling:

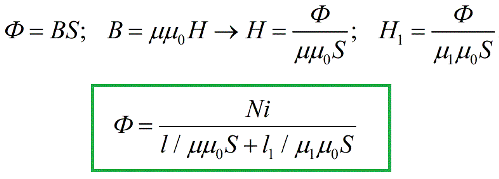
We hebben een formule verkregen die sterk lijkt op de formule die bekend is in de elektrotechniek Wet van Ohm voor een deel van een gesloten circuit, en de rol van de EMF wordt hier gespeeld door de grootheid iN, de magnetomotorische kracht (of MDF) genoemd naar analogie met de elektromotorische kracht. In het SI-systeem wordt de magnetomotorische kracht gemeten in ampère.

De som in de noemer is niets meer dan een analogie van de totale elektrische weerstand voor een elektrisch circuit, en voor een magnetisch circuit wordt het dienovereenkomstig de totale magnetische weerstand genoemd. De termen in de noemer zijn de magnetische weerstanden van individuele secties van het magnetische circuit.

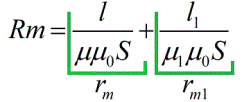
Magnetische weerstanden zijn afhankelijk van de lengte van het magnetische circuit, het dwarsdoorsnede-oppervlak en de magnetische permeabiliteit (vergelijkbaar met elektrische geleidbaarheid voor de gebruikelijke wet van Ohm).Als gevolg hiervan kun je de formule van de wet van Ohm schrijven, alleen voor een magnetisch circuit:

Dat wil zeggen, de formulering van de wet van Ohm met betrekking tot een magnetisch circuit klinkt als volgt: "in een magnetisch circuit zonder vertakking is de magnetische flux gelijk aan het quotiënt van de deling van MDS door de totale magnetische weerstand van het circuit."

Uit de formules blijkt duidelijk dat de magnetische weerstand in NO wordt gemeten in weber ampère, en de totale magnetische weerstand van een magnetisch circuit is numeriek gelijk aan de som van de magnetische weerstanden van de delen van dat magnetische circuit.

De beschreven situatie geldt voor een onvertakt magnetisch circuit dat een willekeurig aantal onderdelen bevat, op voorwaarde dat de magnetische flux achtereenvolgens al deze onderdelen doordringt. Als de magnetische kernen in serie zijn geschakeld, wordt de totale magnetische weerstand gevonden door de magnetische weerstanden van de onderdelen op te tellen.

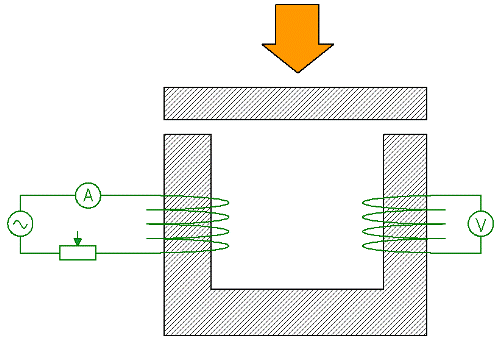
Beschouw nu een experiment dat het effect aantoont van de terughoudendheid van delen van een schakeling op de totale terughoudendheid van een schakeling.Een U-vormige magnetische schakeling wordt gemagnetiseerd door spoel 1, die (wisselstroom) wordt gevoed door een ampèremeter en een reostaat. Een EMF wordt geïnduceerd in de secundaire wikkeling 2 en de aflezingen van de voltmeter die op de wikkeling is aangesloten, zijn, zoals u weet, evenredig met de magnetische flux in het magnetische circuit.

Als je nu de stroom in de primaire wikkeling onveranderd houdt door deze te regelen met een reostaat, en tegelijkertijd de ijzeren plaat tegen het bovenliggende magnetische circuit drukt, nadat de totale magnetische weerstand van het circuit sterk is verminderd, zal de aflezing van de voltmeter zal dienovereenkomstig toenemen.

Natuurlijk zijn de bovenstaande termen, zoals "magnetoweerstand" en "magnetomotorische kracht", formele concepten, aangezien niets in de magnetische flux beweegt, er geen bewegende deeltjes zijn, het is slechts een visuele weergave (zoals een vloeistofstroommodel) van een beter begrip van de wetten...

De fysieke betekenis van het bovenstaande experiment en andere soortgelijke experimenten is om te begrijpen hoe de introductie van niet-magnetische spleten en magnetische materialen in het magnetische circuit de magnetische flux in het magnetische circuit beïnvloedt.

Door bijvoorbeeld een magneet in een magnetisch circuit te introduceren, voegen we extra moleculaire stromen toe aan de lichamen die zich al in het circuit bevinden, die extra magnetische fluxen introduceren. Formele concepten zoals "magnetische weerstand" en "magnetische kracht" blijken erg handig te zijn bij het oplossen van een praktisch probleem, en daarom worden ze met succes gebruikt in de elektrotechniek.