Wet van behoud van energie

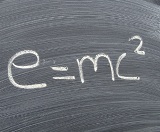De moderne natuurkunde kent vele soorten energie die verband houden met beweging of een verschillende onderlinge opstelling van een grote verscheidenheid aan materiële lichamen of deeltjes. Elk bewegend lichaam heeft bijvoorbeeld kinetische energie die evenredig is met het kwadraat van zijn snelheid. Deze energie kan veranderen als de snelheid van het lichaam toeneemt of afneemt. Een lichaam dat boven de grond is geheven, heeft een potentiële zwaartekrachtenergie variërend van drie veranderingen in de hoogte van het lichaam.

Stationaire elektrische ladingen die zich op enige afstand van elkaar bevinden, hebben een elektrostatische potentiële energie in overeenstemming met het feit dat, volgens de wet van Coulomb, de ladingen elkaar aantrekken (als ze een verschillend teken hebben) of afstoten met een kracht die omgekeerd evenredig is met het kwadraat van de afstand daartussen.

Kinetische en potentiële energie wordt bezeten door moleculen, atomen en deeltjes, hun bestanddelen - elektronen, protonen, neutronen, enz. in de vorm van mechanisch werk, in de stroom van elektrische stroom, in de overdracht van warmte, in de verandering van de interne toestand van lichamen, in de voortplanting van elektromagnetische golven, enz.

Meer dan 100 jaar geleden werd een fundamentele natuurwet opgesteld, volgens welke energie niet kan verdwijnen of uit het niets kan ontstaan. Ze kan alleen van het ene type in het andere veranderen…. Deze wet wordt de wet van behoud van energie genoemd.

In de werken van A. Einstein is deze wet aanzienlijk ontwikkeld. Einstein stelde de uitwisselbaarheid van energie en massa vast en breidde daarmee de interpretatie uit van de wet van behoud van energie, die nu algemeen wordt aangeduid als de wet van behoud van energie en massa.

In overeenstemming met de theorie van Einstein is elke verandering in de lichaamsenergie dE gerelateerd aan een verandering in de massa dm door de formule dE = dmc2, waarbij c de lichtsnelheid is in een vacuüm gelijk aan 3 x 108 Miss.

Met name uit deze formule volgt dat als als gevolg van een proces de massa van alle bij het proces betrokken lichamen met 1 g afneemt, de energie gelijk is aan 9 × 1013 J, wat overeenkomt met 3000 ton standaard brandstof.

Deze verhoudingen zijn van primair belang bij de analyse van nucleaire transformaties. Bij de meeste macroscopische processen kan de verandering in massa worden verwaarloosd en kan alleen over de wet van behoud van energie worden gesproken.

Laten we de transformaties van energie volgen aan de hand van een concreet voorbeeld. Overweeg de hele keten van energieomzettingen die nodig zijn om een ​​onderdeel op een draaibank te produceren (fig. 1). Stel dat de initiële energie 1, waarvan we de hoeveelheid voor 100% nemen, wordt verkregen door de volledige verbranding van een bepaalde hoeveelheid fossiele brandstof. Daarom zit voor ons voorbeeld 100% van de initiële energie in de producten van brandstofverbranding, die een hoge temperatuur hebben (ongeveer 2000 K).

De verbrandingsproducten in de ketel van de energiecentrale geven bij afkoeling hun interne energie in de vorm van warmte af aan water en waterdamp. Om technische en economische redenen kunnen de verbrandingsproducten echter niet worden afgekoeld tot omgevingstemperatuur. Ze worden door de buis de atmosfeer in geworpen bij een temperatuur van ongeveer 400 K, waarbij ze een deel van de oorspronkelijke energie meenemen. Daarom wordt slechts 95% van de initiële energie overgedragen aan de interne energie van de waterdamp.

De resulterende waterdamp komt de stoomturbine binnen, waar de interne energie aanvankelijk gedeeltelijk wordt omgezet in kinetische energie van de stoomstrings, die vervolgens als mechanische energie wordt overgedragen aan de turbinerotor.

Slechts een deel van de stoomenergie kan worden omgezet in mechanische energie. De rest wordt aan het koelwater gegeven wanneer stoom wordt gecondenseerd in de condensor. In ons voorbeeld gingen we ervan uit dat de energie die naar de turbinerotor wordt overgebracht ongeveer 38% zou zijn, wat ongeveer overeenkomt met de stand van zaken in moderne energiecentrales.

Bij het omzetten van mechanische energie in elektrische energie door de zogenaamde Joule-verliezen in de rotor- en statorwikkelingen van de generator zullen ongeveer 2% van de energie verliezen. Als gevolg hiervan gaat ongeveer 36% van de initiële energie naar het net.

Een elektromotor zal slechts een deel van de geleverde elektrische energie omzetten in mechanische energie om de draaibank te laten draaien. In ons voorbeeld zal ongeveer 9% van de energie in de vorm van Joule-warmte in de motorwikkelingen en wrijvingswarmte in de lagers worden afgegeven aan de omringende atmosfeer.

Zo wordt slechts 27% van de initiële energie geleverd aan de werkende organen van de machine. Maar daar houden de energie-ongelukken ook niet op. Het blijkt dat de meeste energie tijdens het bewerken van een onderdeel wordt besteed aan wrijving en in de vorm van warmte wordt afgevoerd met de vloeistof die het onderdeel afkoelt. Theoretisch zou slechts een zeer kleine fractie (in ons voorbeeld wordt uitgegaan van 2%) van de initiële energie voldoende zijn om het gewenste deel van het originele onderdeel te verkrijgen.

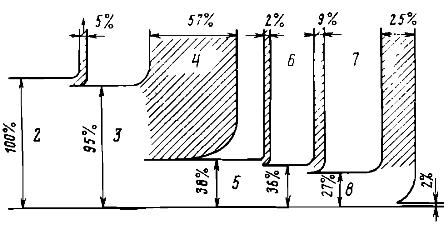
Rijst. 1. Schema van energietransformaties tijdens de verwerking van een werkstuk op een draaibank: 1 — energieverlies met uitlaatgassen, 2 — interne energie van verbrandingsproducten, 3 — interne energie van de werkvloeistof — waterdamp, 4 — warmte die vrijkomt bij de koeling water in een turbinecondensor, 5 — mechanische energie van de rotor van een turbinegenerator, 6 — verliezen in de elektrische generator, 7 — afval in de elektrische aandrijving van de machine, 8 — mechanische rotatie-energie van de machine, 9 — wrijving werk, dat wordt omgezet in warmte, gescheiden van de vloeistof, het koelgedeelte, 10 - verhoging van de interne energie van het onderdeel en de chips na verwerking ...

Er kunnen ten minste drie zeer bruikbare conclusies worden getrokken uit het voorbeeld in kwestie, als het als redelijk typisch wordt beschouwd.

Ten eerste gaat bij elke stap van de energieconversie een deel ervan verloren... Deze bewering moet niet worden opgevat als een overtreding van de wet van behoud van energie. Het gaat verloren vanwege het nuttige effect waarvoor de overeenkomstige transformatie wordt uitgevoerd. De totale hoeveelheid energie na de omzetting blijft ongewijzigd.

Als het proces van energieomzetting en -overdracht plaatsvindt in een bepaalde machine of apparaat, dan wordt de efficiëntie van dit apparaat meestal gekenmerkt door efficiëntie (efficiëntie)\u200b Een diagram van zo'n apparaat wordt getoond in Fig. 2.

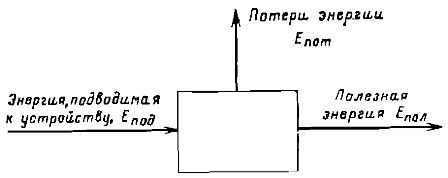
Rijst. 2. Schema voor het bepalen van het rendement van een apparaat dat energie omzet.

Met behulp van de in de afbeelding getoonde notatie kan de efficiëntie worden gedefinieerd als Efficiëntie = Epol/Epod

Het is duidelijk dat er in dit geval, gebaseerd op de wet van behoud van energie, Epod = Epol + Epot moet zijn

Daarom kan het rendement ook als volgt worden geschreven: rendement = 1 — (Epot / Epol)

Terugkerend naar het voorbeeld getoond in FIG. 1, kunnen we zeggen dat de efficiëntie van de ketel 95% is, de efficiëntie van het omzetten van de interne energie van stoom in mechanisch werk is 40%, de efficiëntie van de elektrische generator is 95%, de efficiëntie is — de elektrische aandrijving van een machine — 75%, en de efficiëntie van de daadwerkelijke verwerking van het werkstuk is ongeveer 7%.

In het verleden, toen de wetten van energietransformatie nog niet bekend waren, was het de droom van mensen om een ​​zogenaamde perpetuum mobile te maken - een apparaat dat nuttig werk zou doen zonder energie te verbruiken. Zo'n hypothetische motor, waarvan het bestaan ​​de wet van behoud van energie zou schenden, wordt tegenwoordig een perpetuum mobile van de eerste soort genoemd, in tegenstelling tot een perpetuum mobile van de tweede soort. serieus de mogelijkheid om een ​​perpetuum mobile van de eerste soort te creëren.

Ten tweede worden alle energieverliezen uiteindelijk omgezet in warmte, die wordt afgegeven aan atmosferische lucht of aan water uit natuurlijke reservoirs.

Ten derde gebruiken mensen uiteindelijk maar een klein deel van de primaire energie die wordt verbruikt om het relevante gunstige effect te verkrijgen.

Dit is met name duidelijk als we kijken naar de transportkosten van energie. In geïdealiseerde mechanica, die geen rekening houdt met wrijvingskrachten, hebben bewegende lasten in het horizontale vlak geen energie nodig.

In reële omstandigheden wordt alle door een voertuig verbruikte energie gebruikt om wrijvingskrachten en luchtweerstandskrachten te overwinnen, dat wil zeggen dat uiteindelijk alle energie die tijdens het transport wordt verbruikt, wordt omgezet in warmte. In dit opzicht zijn de volgende cijfers interessant, die het werk karakteriseren van het verplaatsen van 1 ton vracht over een afstand van 1 km met verschillende soorten transport: vliegtuig - 7,6 kWh / (t-km), auto - 0,51 kWh / ( t- km) , trein-0,12 kWh/(t-km).

Zo kan hetzelfde gunstige effect worden bereikt met luchtvervoer ten koste van 60 keer meer energieverbruik dan met spoor. Natuurlijk geeft een hoog energieverbruik een flinke tijdswinst, maar zelfs bij dezelfde snelheid (auto en trein) verschillen de energiekosten 4 keer.

Dit voorbeeld suggereert dat mensen vaak compromissen sluiten met energie-efficiëntie om andere doelen te bereiken, bijvoorbeeld comfort, snelheid, enz. In de regel is de energie-efficiëntie van het proces zelf van weinig belang voor ons — de algemene technische en economische evaluaties van de efficiëntie van processen zijn belangrijk... Maar naarmate de prijs van primaire energiecomponenten stijgt, wordt de energiecomponent in technische en economische evaluaties steeds belangrijker.