Bepaling van het motorvermogen tijdens repetitieve transiënte werking
 De werkingsmodus van de elektrische aandrijving, waarbij de werkingsperioden zo lang zijn en zo worden afgewisseld met pauzes van een bepaalde duur, dat de temperatuur van alle apparaten waaruit de elektrische aandrijving bestaat geen stabiele waarde bereikt, noch tijdens elke werkperiode, noch tijdens elke pauze wordt onderbroken.
De werkingsmodus van de elektrische aandrijving, waarbij de werkingsperioden zo lang zijn en zo worden afgewisseld met pauzes van een bepaalde duur, dat de temperatuur van alle apparaten waaruit de elektrische aandrijving bestaat geen stabiele waarde bereikt, noch tijdens elke werkperiode, noch tijdens elke pauze wordt onderbroken.
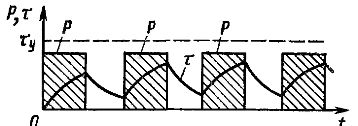
Het periodieke belastingsregime komt overeen met grafieken die vergelijkbaar zijn met die getoond in Fig. 1. De oververhitting van de elektromotor varieert langs de stippellijn van een zaag die bestaat uit afwisselende segmenten van verwarmings- en koelcurven. De intermitterende laadmodus is typerend voor de meeste aandrijvingen van machinegereedschappen.
Rijst. 1. Periodiek laadschema
Het vermogen van een elektromotor die in periodieke modus werkt, wordt het gemakkelijkst bepaald door de formule voor gemiddelde verliezen, die kan worden geschreven als
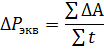
waarbij ΔA het energieverlies is bij elke belastingswaarde, inclusief de start- en stopprocessen.
Als de elektromotor niet werkt, verslechteren de koelomstandigheden aanzienlijk. Hiermee wordt rekening gehouden door experimentele coëfficiënten β0 <1 te introduceren. De pauzetijd t0 wordt vermenigvuldigd met de coëfficiënt β0, waardoor de noemer van de formule afneemt en de equivalente verliezen ΔREKV toenemen en dienovereenkomstig neemt het nominale vermogen van de elektromotor toe.
Voor asynchrone beveiligde motoren van de A-serie met een synchroon toerental van 1500 tpm en een vermogen van 1-100 kW, is de β0-coëfficiënt 0,50-0,17 en voor spuimotoren β0 = 0,45-0,3 (met een toename in Пн , coëfficiënt β0 afneemt). Voor gesloten motoren ligt β0 dicht bij de eenheid (0,93-0,98). Dit komt doordat het ventilatierendement van gesloten motoren laag is.
Bij het starten en stoppen is het gemiddelde toerental van de elektromotor lager dan het nominale, waardoor ook de koeling van de elektromotor verslechtert, wat gekenmerkt wordt door de coëfficiënt

Bij het bepalen van de coëfficiënt β1 wordt voorwaardelijk aangenomen dat de verandering in de rotatiefrequentie verloopt volgens een lineaire wet en dat de coëfficiënt β1 er lineair van afhangt.
Als we de coëfficiënten β0 en β1 kennen, krijgen we
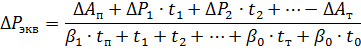
waarbij ΔР1, ΔР2, — vermogensverliezen bij verschillende belastingen, kW; t1 t2 — actietijd van deze belastingen, s; tn, tT, t0 — start-, vertragings- en pauzetijd, s; ΔАп ΔАТ — energieverliezen in de motor tijdens starten en stoppen, kJ.
Zoals hierboven vermeld, moet elke motor worden geselecteerd op verwarming en overbelasting. Om de methode van gemiddelde verliezen toe te passen, is het noodzakelijk om vooraf een bepaalde elektromotor in te stellen, die in dit geval ook wordt aanbevolen om te worden geselecteerd op basis van de overbelastingsomstandigheden.De equivalente vermogensformule kan worden gebruikt voor een ruwe berekening in gevallen waarin starten en stoppen zelden voorkomt en geen significante invloed heeft op de verwarming van de elektromotor.
In de machinebouw worden voor gebruik in intermitterende belastingsmodus elektromotoren gebruikt die zijn ontworpen om met een continue belasting te werken. De elektrische industrie produceert ook motoren die speciaal zijn ontworpen om intermitterende belastingen te verwerken, die veel worden gebruikt in hef- en transportconstructies. Dergelijke elektromotoren worden geselecteerd rekening houdend met de relatieve opnameduur:

waarbij tp de looptijd van de motor is; t0 — pauzeduur.
Een voorbeeld van het kiezen van een motor op vermogen in meerdere kortstondige bedrijfsmodi.
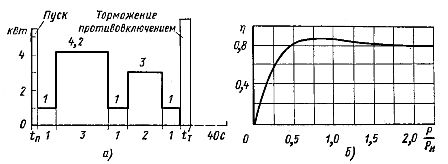
Bepaal het vermogen van de elektromotor bij n0 — 1500 tpm; de motor werkt volgens het belastingsschema getoond in afb. 2, een. Asvermogen van de elektromotor bij stationair draaiende machine Pxx = 1 kW. Verminderd traagheidsmoment van de machine Jc = 0,045 kg-m2.
Antwoord:
1. Selecteer de elektromotor volgens de overbelastingsomstandigheden, bijvoorbeeld λ = 1,6:

Volgens de catalogus kiezen we een elektromotor met de beschermde versie van het dichtstbijzijnde hoge vermogen (2,8 kW), waarbij mon = 1420 tpm;

Voor deze motor is λ = 0,85 • 2 = 1,7. Op deze manier wordt de motor geselecteerd met een bepaalde overbelastingslimiet.
De afhankelijkheid η = f (P / Pн) van deze motor wordt getoond in Fig. 2, geb.
Rijst. 2. Afhankelijkheden N = f (t) en η = f (P / Pн)
2. Volgens de formule
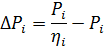
we detecteren verliezen bij machten 1; 3; 4,2 kW (volgens schema). De verliezen zijn respectievelijk 0,35; 0,65 en 1 kW. We vinden verliezen bij Pn = 2,8 kW, die ΔPn = 0,57 kW zijn.
3. Bepaal de starttijd en stoptijd door oppositie:
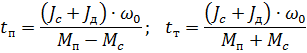
waar:
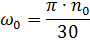
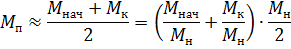



We krijgen tn = 0,30 s; tt = 0,21 s.
4. Bepaal de start- en stopverliezen:

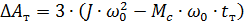
We krijgen ΔAp = 1,8 kJ en ΔAt = 3,8 kJ.
5. Zoek de equivalente verliezen in de lus:
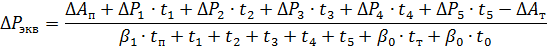
waar
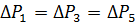
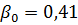
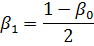
We krijgen ΔREKV = 0,44 kW. Aangezien ΔPn = 0,57, dan is ΔREKV <ΔPn en daarom is de motor correct geselecteerd.