Driehoeken van spanningen, weerstanden en vermogens

Iedereen die een idee heeft van vectordiagrammen zal gemakkelijk opmerken dat er heel duidelijk een rechthoekige spanningsdriehoek op te onderscheiden is, waarvan elke zijde weerspiegelt: de totale spanning van het circuit, de spanning van de actieve weerstand en de spanning op reactantie.

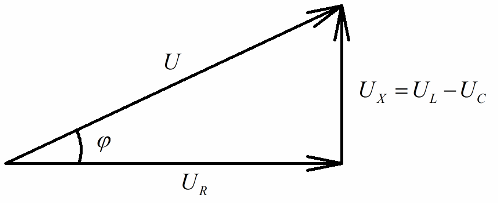
In overeenstemming met de stelling van Pythagoras ziet de relatie tussen deze spanningen (tussen de totale spanning van het circuit en de spanning van de secties) er als volgt uit:

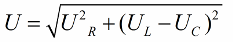
Als de volgende stap is om de waarden van deze spanningen te delen door de stroom (de stroom vloeit gelijk door alle secties van de serieschakeling), dan door De wet van Ohm we krijgen de weerstandswaarden, dat wil zeggen, nu kunnen we praten over een rechthoekige driehoek van weerstanden:

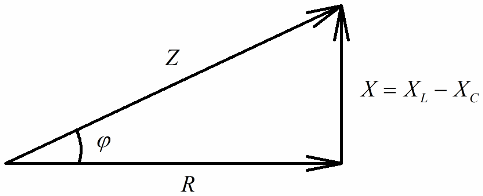
Op een vergelijkbare manier (zoals in het geval van spanningen), met behulp van de stelling van Pythagoras, is het mogelijk om een ​​relatie vast te stellen tussen de impedantie van het circuit en de reactanties. De relatie wordt uitgedrukt door de volgende formule:

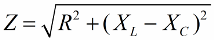
Vervolgens vermenigvuldigen we de weerstandswaarden met de stroom, in feite zullen we elke zijde van de rechthoekige driehoek een bepaald aantal keren vergroten. Als resultaat krijgen we een rechthoekige driehoek met capaciteiten:

Het actieve vermogen dat vrijkomt bij de actieve weerstand van het circuit geassocieerd met de onomkeerbare omzetting van elektrische energie (in warmte, bij het uitvoeren van werkzaamheden in de installatie) zal duidelijk gerelateerd zijn aan het blindvermogen dat betrokken is bij de omkeerbare omzetting van energie (het creëren van magnetische en elektrische velden in spoelen en condensatoren) en met volledige voeding van de elektrische installatie.

Actief vermogen wordt gemeten in watt (W), reactief vermogen - in varis (VAR - volt-ampère reactief), totaal - in VA (volt-ampère).

Volgens de stelling van Pythagoras hebben we het recht om te schrijven:

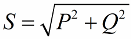
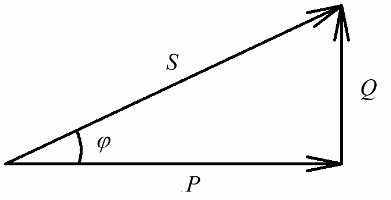
Laten we nu aandacht besteden aan het feit dat er in de machtsdriehoek een hoek phi is, waarvan de cosinus gemakkelijk te bepalen is, voornamelijk door actief vermogen en schijnbaar vermogen. De cosinus van deze hoek (cos phi) arbeidsfactor genoemd. Het laat zien hoeveel van het totale vermogen wordt verantwoord bij het uitvoeren van nuttig werk in een elektrische installatie en niet wordt teruggeleverd aan het net.

Vanzelfsprekend duidt een hogere arbeidsfactor (maximaal één) op een hogere omzettingsefficiëntie van de energie die aan de installatie wordt geleverd voor werking. Als de arbeidsfactor 1 is, wordt alle geleverde energie gebruikt om arbeid te verrichten.

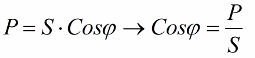
De verkregen verhoudingen laten toe om het stroomverbruik van de installatie uit te drukken in termen van arbeidsfactor, actief vermogen en netspanning:

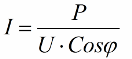
Dus hoe kleiner de cosinus phi, hoe meer stroom het netwerk nodig heeft om een ​​bepaalde taak uit te voeren. In de praktijk beperkt deze factor (maximale netwerkstroom) de transmissiecapaciteit van de transmissielijn en daarom geldt: hoe lager de arbeidsfactor, hoe groter de lijnbelasting en hoe lager de bruikbare bandbreedte (de lage cosinus phi leidt tot beperking). Joule-verliezen in hoogspanningslijnen met afnemende cosinus phi kunnen worden afgeleid uit de volgende formule:

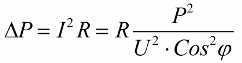
Op de actieve weerstand R van de transmissielijn nemen de verliezen toe naarmate de stroom I hoger is, ook al reageert deze op de belasting. Daarom kunnen we zeggen dat met een lage arbeidsfactor de kosten van elektriciteitstransmissie gewoon toenemen. Dit betekent dat het verhogen van cosinus phi een belangrijke nationale economische taak is.

Het is wenselijk dat de reactieve component van het totale vermogen nul nadert.Om dit te doen, zou het goed zijn om elektromotoren en transformatoren altijd bij volledige belasting te gebruiken en ze aan het einde van het gebruik uit te schakelen, zodat ze niet inactief zijn. Zonder belasting hebben motoren en transformatoren een zeer lage arbeidsfactor. Een manier om cosinus phi bij gebruikers te verhogen, is door te gebruiken condensator banken En synchrone compensatoren.