Logische apparaten

Logische algebra of Booleaanse algebra wordt gebruikt om de werkingswetten van digitale schakelingen te beschrijven. De algebra van de logica is gebaseerd op het concept van een "gebeurtenis" die al dan niet kan plaatsvinden. Een gebeurtenis die heeft plaatsgevonden wordt als waar beschouwd en een logisch niveau «1» wordt uitgedrukt, een gebeurtenis die niet heeft plaatsgevonden wordt als onwaar beschouwd en een logisch niveau «0» wordt uitgedrukt.

De gebeurtenis wordt beïnvloed door variabelen en zij beïnvloeden volgens een bepaalde wet. Deze wet wordt een logische functie genoemd, de variabelen zijn argumenten... Che. de logische functie is de functie y = f (x1, x2, … xn), die de waarden «0» of «1» aanneemt. De variabelen x1, x2, … xn hebben ook waarden «0» of «1».

Algebra van logica - een tak van wiskundige logica die de structuur van complexe logische beweringen bestudeert en manieren om hun waarheid vast te stellen door middel van algebraïsche methoden. In de formules van logische algebra zijn de variabelen logisch of binair, dat wil zeggen dat ze slechts twee waarden aannemen - onwaar en waar, die respectievelijk worden aangeduid met 0 en 1. Elk computerprogramma bevat logische bewerkingen.

Apparaten die zijn ontworpen om functies van de logische algebra te vormen, worden logische apparaten genoemd. Een logisch apparaat heeft een willekeurig aantal ingangen en slechts één uitgang (figuur 1).

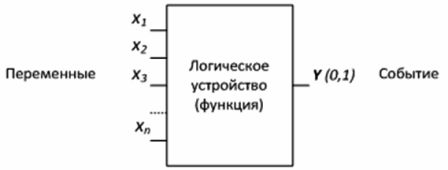
Figuur 1 — Logisch apparaat

Een elektronisch combinatieslot bevat bijvoorbeeld een logisch apparaat waarvoor gebeurtenis (y) het openen van het slot is. Om de gebeurtenis (y = 1) te laten plaatsvinden, d.w.z. het slot is geopend, het is noodzakelijk om de variabelen te definiëren - tien knoppen op het numerieke toetsenbord. Bepaalde knoppen moeten worden ingedrukt, bijv. neem de waarde «1» en druk tegelijkertijd in een bepaalde volgorde - een logische functie.

Het is handig om elke logische functie weer te geven in de vorm van een toestandstabel (waarheidstabel), waarin mogelijke combinaties van variabelen (argumenten) en de overeenkomstige waarde van de functie worden vastgelegd.

Logische apparaten zijn gebouwd op logische poorten die een specifieke functie vervullen. De fundamentele logische functies zijn logische optelling, logische vermenigvuldiging en logische ontkenning.

1) OF (OF) — logische toevoeging of deling (van het Engelse disjunctie — onderbreking) — een logische eenheid verschijnt aan de uitvoer van dit element wanneer een eenheid ten minste aan één van de invoer verschijnt. De uitgang zal alleen logisch nul zijn als er een logisch nulsignaal is op alle ingangen.

Deze bewerking kan worden uitgevoerd met behulp van een contactcircuit met twee parallel geschakelde contacten. «1» aan de uitgang van zo'n circuit zal verschijnen als minstens één van de contacten gesloten is.

2) AND (AND) — logische vermenigvuldiging of verbinding (van de Engelse unie — verbinding, & — ampersand) — aan de uitgang van dit element verschijnt het signaal van een logische eenheid alleen wanneer een logische eenheid aanwezig is op alle ingangen.Als ten minste één invoer nul is, is de uitvoer ook nul.

Deze bewerking kan worden uitgevoerd door een contactcircuit bestaande uit in serie geschakelde contacten.

3) NOT — logische ontkenning of inversie aangegeven door een streepje boven een variabele — de bewerking wordt uitgevoerd op één variabele x en de waarde van y is het tegenovergestelde van die variabele.

De operatie kan NIET worden uitgevoerd met een normaal gesloten contact van het elektromagnetische relais: er staat geen spanning op de relaisspoel (x = 0) — het contact is ook gesloten aan de uitgang «1» (y = 1). Bij aanwezigheid van spanning op de relaisspoel (x = 1) is het contact ook open op uitgang «0» (y = 0).

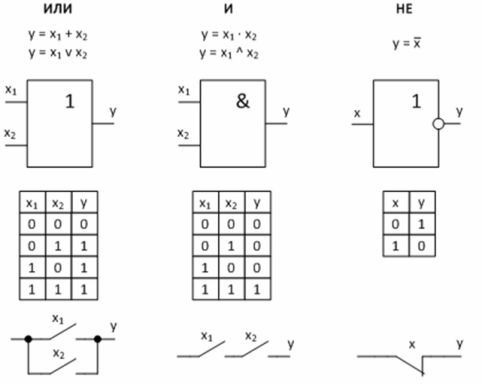
Figuur 2 — Fundamentele logische functies en hun implementatie

Logische apparaten gebruiken verschillende logische poorten. Bijzonder belangrijk zijn twee universele logische bewerkingen, die elk onafhankelijk elke logische functie kunnen vormen.

4) NAND — Schaefer-functie.

5) OF NIET — Ponsfunctie.

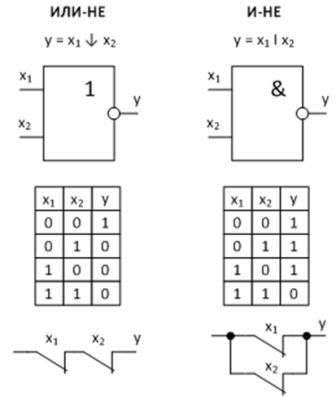
Figuur 3 — Universele logische functies en hun implementatie

Voorbeeld: Beveiligingsalarmcircuit op basis van logische elementen. Generator G genereert een sirenesignaal en voert het naar de versterkertrap via het logische element «AND» van de microschakeling DD2. Wanneer de beveiligingsschakelaars S1 — S4 gesloten zijn, werkt het niveau «0» op de ingangen van het element DD1 — het niveau «0» bevindt zich op de onderste ingang van het element «I» DD2, wat betekent dat de poort van de transistor VT is ook «0».

In het geval van het openen van ten minste één van de schakelaars, bijvoorbeeld S1, zal de ingang van het element DD1 via de weerstand R1 een spanning van niveau «1» ontvangen, waardoor het verschijnen van «1» aan de tweede ingang van het element «EN» DD1.Hierdoor kan het signaal van de generator G worden doorgegeven aan de poort van de transistor waarvan de luidspreker de belasting is.

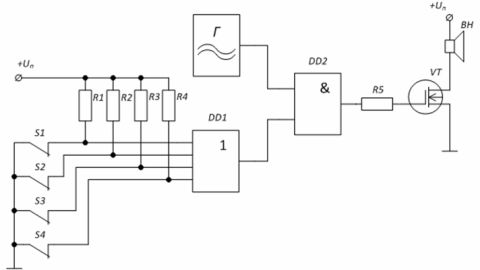
Figuur 4 — Alarmbeveiligingsschema

Complexe digitale circuits worden gebouwd door logische basiscircuits keer op keer te herhalen. Het hulpmiddel voor een dergelijke constructie is Booleaanse algebra, wat in termen van digitale technologie logische algebra wordt genoemd. In tegenstelling tot een variabele in gewone algebra, heeft een booleaanse variabele slechts twee waarden, die booleaanse nul en booleaanse één worden genoemd.

Logische nul en logische één worden aangeduid met 0 en 1. In logische algebra zijn 0 en 1 geen getallen, maar logische variabelen. In logische algebra zijn er drie basisbewerkingen tussen logische variabelen: logische vermenigvuldiging (conjunctie), logische optelling (disjunctie) en logische ontkenning (inversie).

Elektronische schakelingen die dezelfde logische functie vervullen, maar samengesteld met verschillende elementen, verschillend in stroomverbruik, voedingsspanning, waarden van hoge en lage uitgangsspanningsniveaus, signaalvoortplantingsvertragingstijd en draagvermogen.

Zie ook over dit onderwerp: EN, OF, NIET, EN-NIET, OF-NIET logische poorten en hun waarheidstabellen